2020-02-27 12:28:17

Preliminaries

Announcements

Today’s topics

  • Some observations about GitHub use and R Markdown
  • Simulation as a tool for reproducible and transparent science
  • Visualization in R
  • Advanced simulation

Observations

git/GitHub

  • Add .Rproj to your .gitignore. See Natalie’s stub.
  • You’re in charge of what goes where.
  • Public repos are public, but no one knows what you’re doing unless you alert them.

  • Pull first; edit second.
  • Pull requests are when you edit my code and want me to “pull”/adopt it.
    • If I’m a collaborator on the project with write privileges, I don’t have to issue a pull request.

R Markdown

  • Ok to make multiple R Markdown files and link them
  • Make sure to add spaces where they belong: ##Header vs. ## Header
  • Comments! Add them. This is your record of what you did.
  • Don’t forget you can hide things

  • Label chunks
  • Make chunks bite-sized
  • Add comments in your code to explain what you’re doing
    • Could someone else figure out what your code does?

Be a risk-taker; be your own professor

Simulation as a tool for reproducible and transparent science

  • Why simulate
  • What to simulate
  • How to simulate

Why & what to simulate?

  • Explore sample sizes, effect sizes, power
  • Pre-plan/test, polish data-munging workflows
  • Make hypotheses even more explicit
    • Simulation == Pregistration on steroids
    • ‘X affects Y’ -> ‘Mean(X) > Mean(Y)’
    • or ’Mean(X) >= 2*Mean(Y)’
  • Simulate data analysis in advance

  • Plan data visualizations in advance
  • Avoid avoidable errors
  • Plan your work, work your plan
  • Super easy to run analyses when your data come in

How to simulate

  • R functions
  • R Markdown document(s)

Super-simple example

  • Hypothesis 1: Height (inches) is correlated with weight (lbs)

# choose sample size
sample_n <- 200

# choose intercept and slope
beta0 <- 36   # inches
beta1 <- 0.33  # Rick's guess

# choose standard deviation for error
sigma <- 10 # Rick's guess

# random weights between 80 lbs and 250 lbs (uniform sampling)
w <- runif(n = sample_n, min = 80, max = 250)

h_pred <- rep(x = beta0, n = sample_n) + beta1 * w
h <- h_pred + rnorm(n = sample_n, mean = 0, sd = sigma)

library(ggplot2)
library(dplyr)

hist(w)

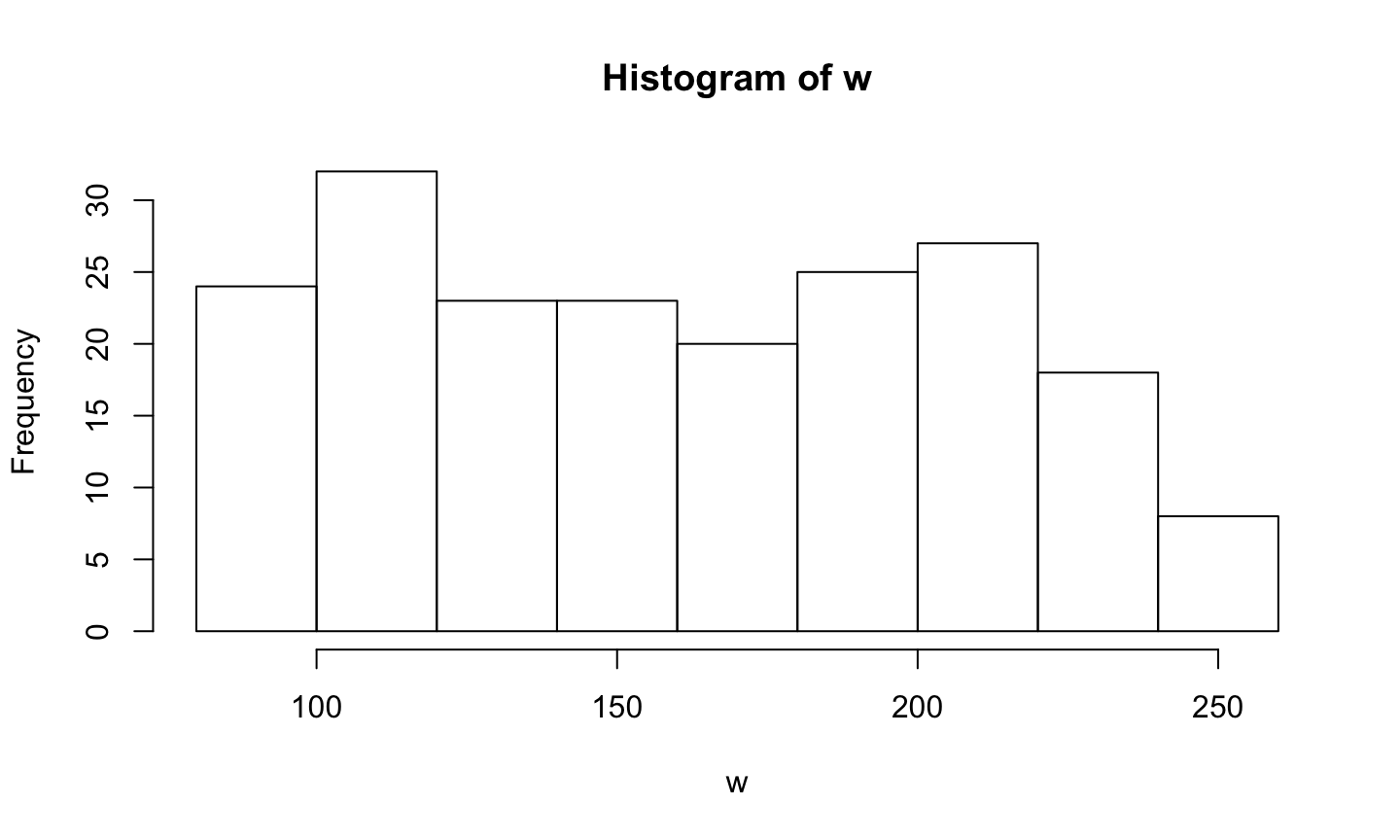
hist(h)

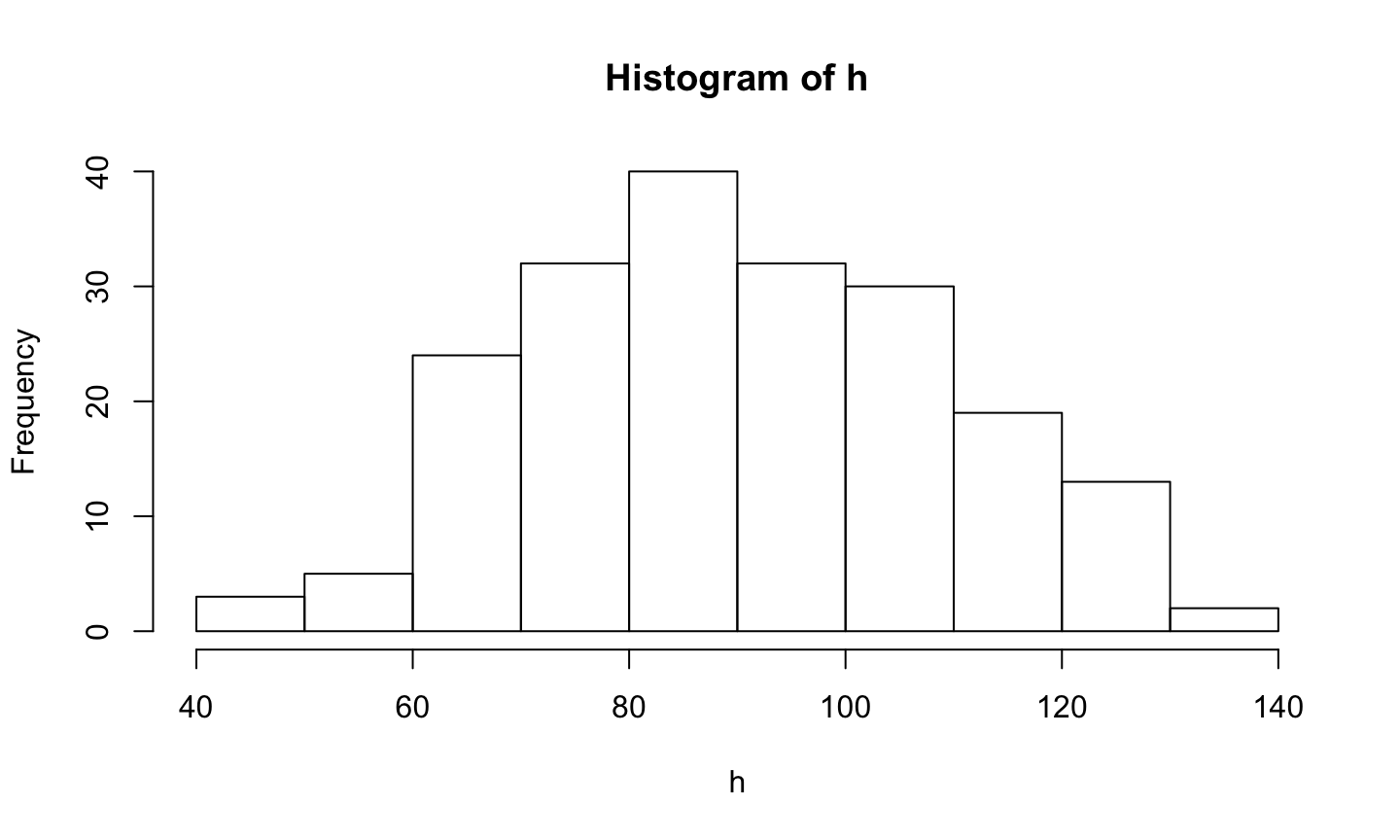
hist(h_pred)

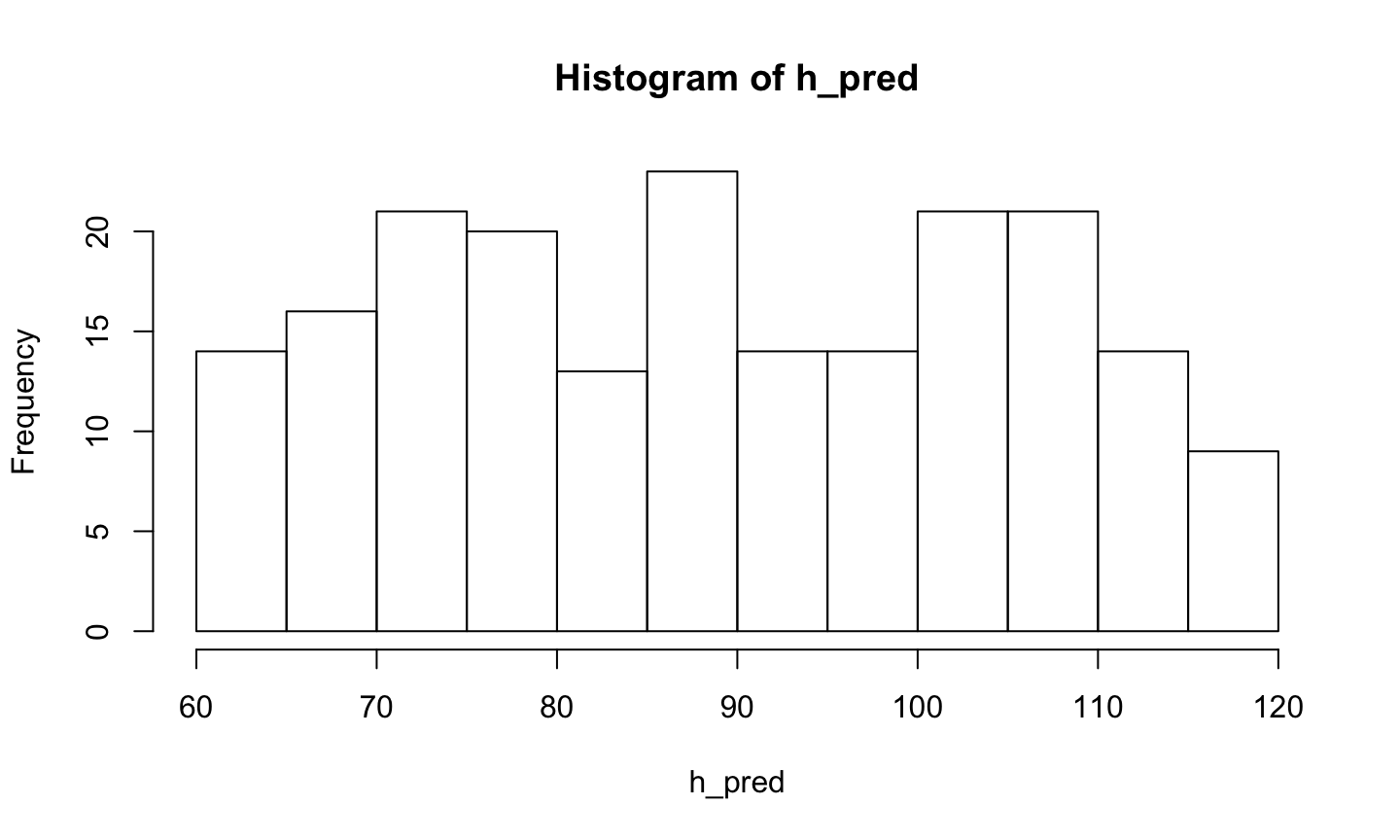
# Put h and w into data frame for ggplot
height_weight <- data.frame(inches = h, lbs = w)

# Plot
scatter_1 <- ggplot2::ggplot(data = height_weight) +
  ggplot2::aes(x = lbs, y = inches) +
  ggplot2::geom_point()
scatter_1

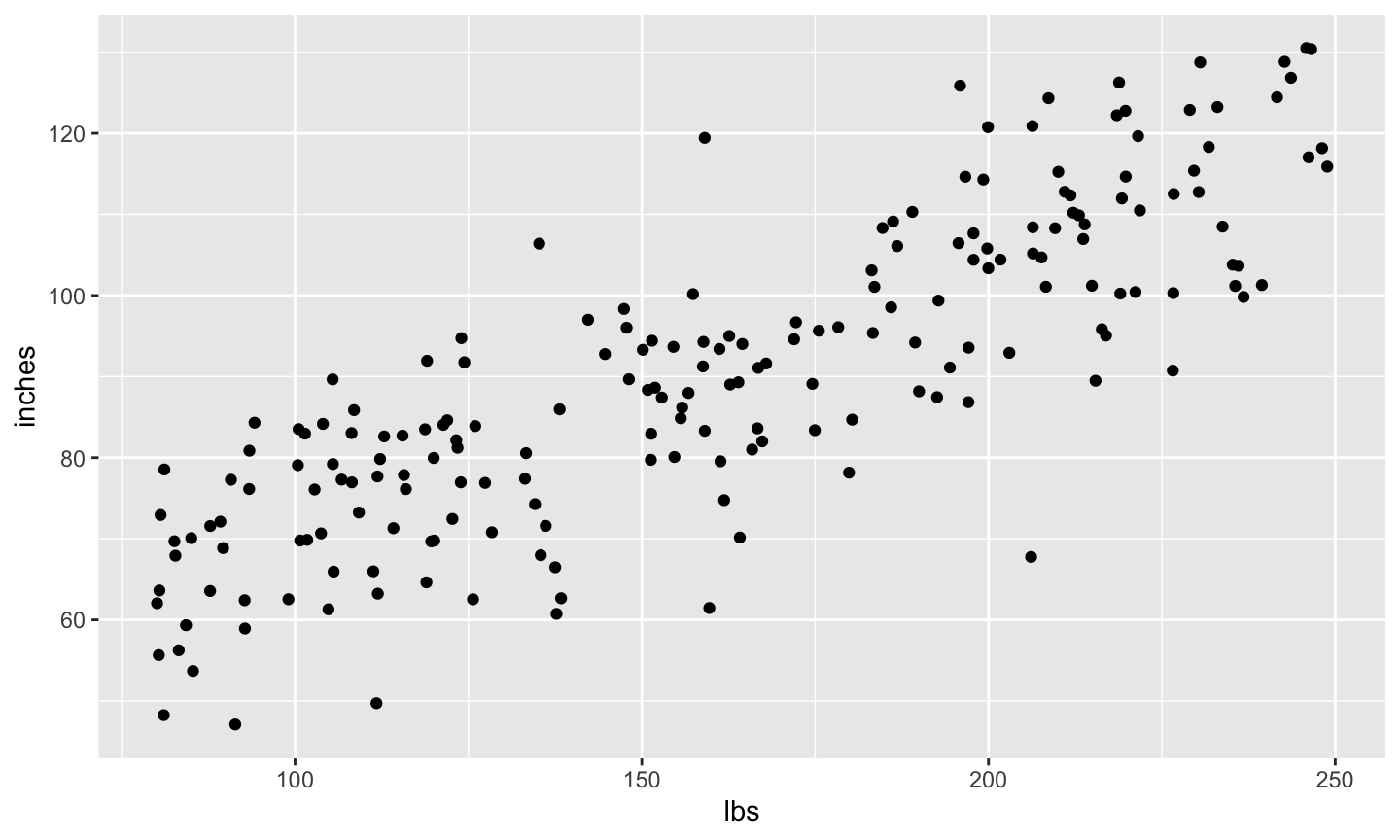
Data pictures

  • What should your data look like if your hypothesis is confirmed?

That’s synthesis, now analysis

  • Remember Hypothesis 1: Height (inches) is correlated with weight (lbs)?
# Could use the raw data
# cor.test(x = w, y = h)
# Or, to use the values in the data frame, use with(...)

with(height_weight, cor.test(x = inches, y = lbs))
## 
##  Pearson's product-moment correlation
## 
## data:  inches and lbs
## t = 21.472, df = 198, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.7892534 0.8737537
## sample estimates:
##       cor 
## 0.8364064

Aside: extracting the statistics to make an interactive report

# Save output as a variable
cor_test_inches_lbs <- with(height_weight, cor.test(x = inches, y = lbs))

# What sort of beast is this?
mode(cor_test_inches_lbs)
## [1] "list"

# Aha, it's a list, this shows me all of the parts
unlist(cor_test_inches_lbs)
##                            statistic.t 
##                     "21.4724896345742" 
##                           parameter.df 
##                                  "198" 
##                                p.value 
##                 "1.33502059642752e-53" 
##                           estimate.cor 
##                    "0.836406407472453" 
##                 null.value.correlation 
##                                    "0" 
##                            alternative 
##                            "two.sided" 
##                                 method 
## "Pearson's product-moment correlation" 
##                              data.name 
##                       "inches and lbs" 
##                              conf.int1 
##                    "0.789253416341088" 
##                              conf.int2 
##                    "0.873753662658475"
# Looks like the t value is the first element
cor_test_inches_lbs[[1]]
##        t 
## 21.47249

The Pearson’s product-moment correlation between height and weight is 0.836, \(t\)(198)=21.472, \(p\)=0.00000, with a 95\(\%\) confidence interval of [0.789, 0.874].

I did some formatting using the sprintf() function to make the numbers look pretty. You may also find format() useful.

sprintf("%.3f", my.var) limits my.var to 3 decimal places; where sprintf("%2.3f", my.var) limits it to 2 digits to the left and 3 to the right.

Now back to analysis with our synthetic data

fit <- lm(formula = inches ~ lbs, data = height_weight)
summary(fit) # Use lm() command to fit formula
## 
## Call:
## lm(formula = inches ~ lbs, data = height_weight)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -37.103  -7.520   0.850   6.759  29.707 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 38.58790    2.51316   15.35   <2e-16 ***
## lbs          0.32149    0.01497   21.47   <2e-16 ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10.44 on 198 degrees of freedom
## Multiple R-squared:  0.6996, Adjusted R-squared:  0.6981 
## F-statistic: 461.1 on 1 and 198 DF,  p-value: < 2.2e-16
(ci <- confint(fit)) # confint() command fits confidence intervals
##                  2.5 %     97.5 %
## (Intercept) 33.6319130 43.5438961
## lbs          0.2919663  0.3510174

Surrounding (ci <- confint(fit)) in parentheses saves variable ci and prints it out.

How’d we do?

Parameter Actual Low Estimate High Estimate
\(\beta0\) 36 33.631913 43.5438961
\(\beta1\) 0.33 0.2919663 0.3510174 

# random weights between 80 lbs and 250 lbs (uniform sampling)
w <- runif(n = sample_n, min = 80, max = 250)

h_pred <- rep(x = beta0, n = sample_n) + beta1 * w
h <- h_pred + rnorm(n = sample_n, mean = 0, sd = sigma)
height_weight <- data.frame(inches = h, lbs = w)

fit <- lm(formula = inches ~ lbs, data = height_weight)
summary(fit)
## 
## Call:
## lm(formula = inches ~ lbs, data = height_weight)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -24.8229  -7.5843   0.0817   6.1271  29.6438 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 34.88577    2.48984   14.01   <2e-16 ***
## lbs          0.33834    0.01465   23.09   <2e-16 ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 9.794 on 198 degrees of freedom
## Multiple R-squared:  0.7293, Adjusted R-squared:  0.7279 
## F-statistic: 533.4 on 1 and 198 DF,  p-value: < 2.2e-16
(ci <- confint(fit)) # saves in variable ci and prints
##                  2.5 %     97.5 %
## (Intercept) 29.9757671 39.7957796
## lbs          0.3094516  0.3672307

Parameter Actual Low Estimate High Estimate
\(\beta0\) 36 29.9757671 39.7957796
\(\beta1\) 0.33 0.3094516 0.3672307

Simulation of neural data

Visualization in R

Plot first, analyze last

  • Why?
  • Mike Meyer told me so
  • Less biased
  • Easier to be transparent and reproducible
  • Want/need to plot eventually anyway
  • If a picture’s worth a thousand words…
  • How?

Things I feel strongly about

  • Plot all of your data
  • Every response, condition, participant
  • What do the plots tell you?
  • Do your plots match your prior ‘data picture’?

How

  • Base graphics
    • plot(x,y) hist(x), coplot()
  • ggplot2
    • Grammar of graphics

Base graphics

  • Try it, maybe you’ll like it
  • plot() takes many types of input
  • So does summary()
  • A little harder to customize

Data visualization with ggplot2

  • ggplot2 is the package; ggplot() is the function call
  • Data can be continuous, ordinal, or nominal
  • Graphs map data \(\rightarrow\) visual elements (aesthetics)
  • {height, weight, gender, rt} \(\rightarrow\) {x, y, color, shape, line type, row, column}
  • ‘Add’ layers to our plot using the + operator

Learning ggplot

Let’s walk through the data visualiation chapter

Other ggplot2 resources

Example from K. Healy talk

## `geom_smooth()` using method = 'loess' and formula 'y ~ x'

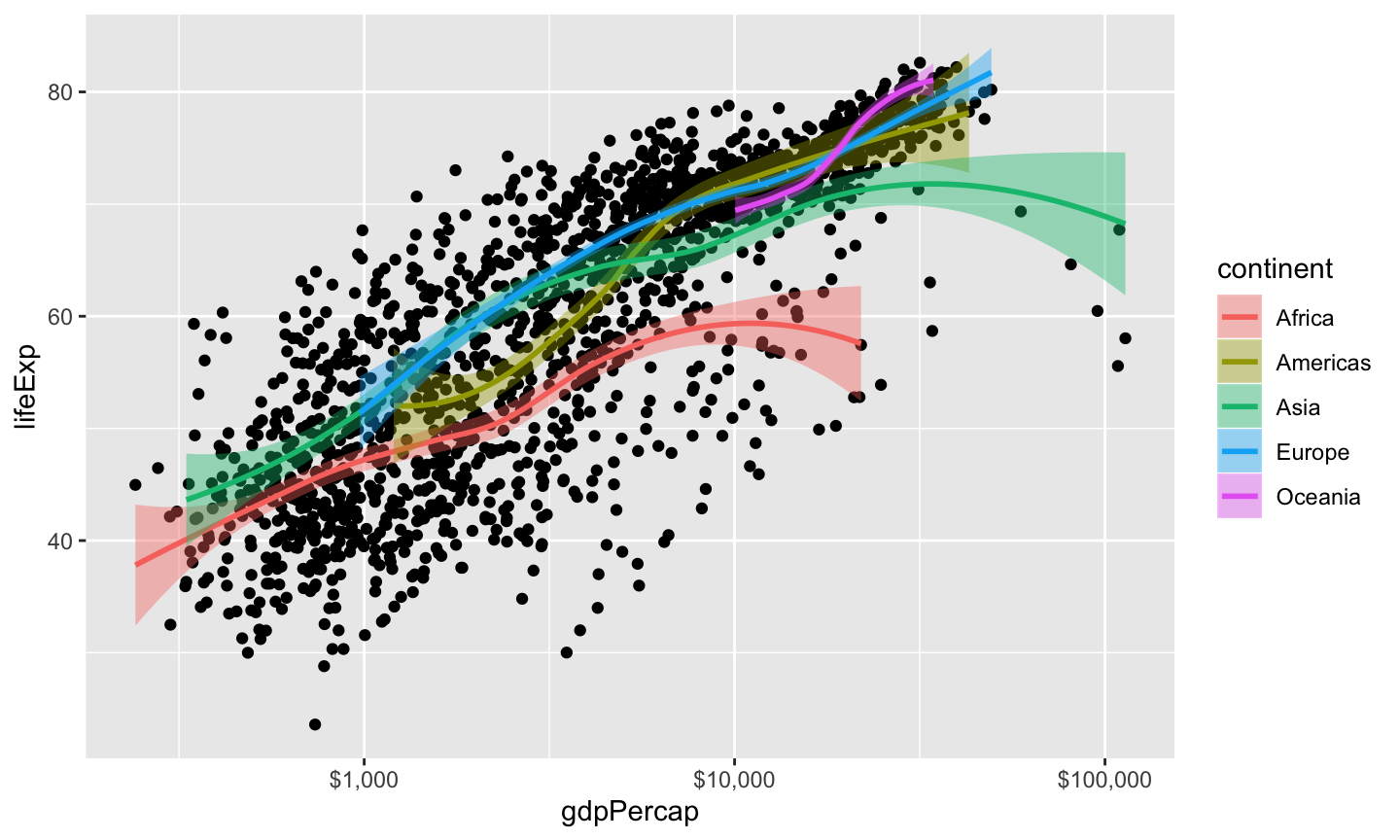
Advanced simulation

Advanced simulation

  • Putting code into a function
  • A factorial design?

Let’s make it a function

  • Functions help automate routines
  • Parts of a function:
    • Input parameters
      • Defaults or not
    • Output(s)
  • my_function_name <- function(my_param1, my_param2 = "cool")

# define global constants from prior simulation
sample_n = 200
beta0 = 36
beta1 = .33
sigma = 10
min_x = 80
max_x = 250

height_weight_sim <- function(sample_n = 200, beta0 = 36, beta1 = .33, sigma = 10, min_x = 80, max_x = 250) {
  # Calculates correlation, intercept, slope estimates for
  # linear relation between two variables
  
  # Args:
  #   sample_n: Number of sample poings, default is 200
  #   beta0: Intercept, default is 36 (inches)
  #   beta1: Slope, default is .33
  #   sigma: Standard deviation of error
  #   min_x: Minimum value for x (weight in lbs)
  #   max_x: Maximum value for x (weight in lbs)
  #
  # Returns:
  #   Named array with values
  #   beta0
  #   beta1
  #   beta0.lo: 2.5% quantile for intercept
  #   beta0.hi  97.5% quantile for intercept
  #   beta1.lo  2.5% quantile for slope
  #   beta1.hi  97.5% quantile for slope

  w <- runif(n = sample_n, min = min_x, max = max_x)

  h_pred <- rep(x = beta0, n = sample_n) + beta1 * w
  h <- h_pred + rnorm(n = sample_n, mean = 0, sd = sigma)
  height.weight <- data.frame(inches = h, lbs = w)

  fit <- lm(formula = inches ~ lbs, data = height.weight)
  ci <- confint(fit)
  
  # Create output vector with named values
  (results <- c("beta0" = beta0, 
    "beta1"= beta1, 
    "beta0.lo" = ci[1,1],
    "beta0.hi" = ci[1,2],
    "beta1.lo" = ci[2,1],
    "beta1.hi" = ci[2,2]))
}

# Defaults only
height_weight_sim()
##      beta0      beta1   beta0.lo   beta0.hi   beta1.lo 
## 36.0000000  0.3300000 30.6497291 40.0010555  0.3066327 
##   beta1.hi 
##  0.3610621
# Larger sample size
height_weight_sim(sample_n = 500)
##      beta0      beta1   beta0.lo   beta0.hi   beta1.lo 
## 36.0000000  0.3300000 33.3918123 39.6015099  0.3081033 
##   beta1.hi 
##  0.3444201

Doing a series of simulations

  • Goal: run our function a number of times, collect the results
n_simulations = 100
n_vars = 6 # variables height_weight_sim() outputs

# initialize output array
height_weight_sim_data <- array(0, dim=c(n_simulations, n_vars))

# Repeat height_weight_sim() n_simulations times
for (i in 1:n_simulations) { 
  height_weight_sim_data[i,] <- height_weight_sim()
  }

# Easier to make simulation data a data frame
ht_wt_sims <- as.data.frame(height_weight_sim_data)

# rename variables to be more easily read
names(ht_wt_sims) <- c("beta0", "beta1", 
                       "beta0.lo", "beta0.hi",
                       "beta1.lo", "beta1.hi")

# Add a variable to index the simulation number
ht_wt_sims$sim_num <- 1:n_simulations

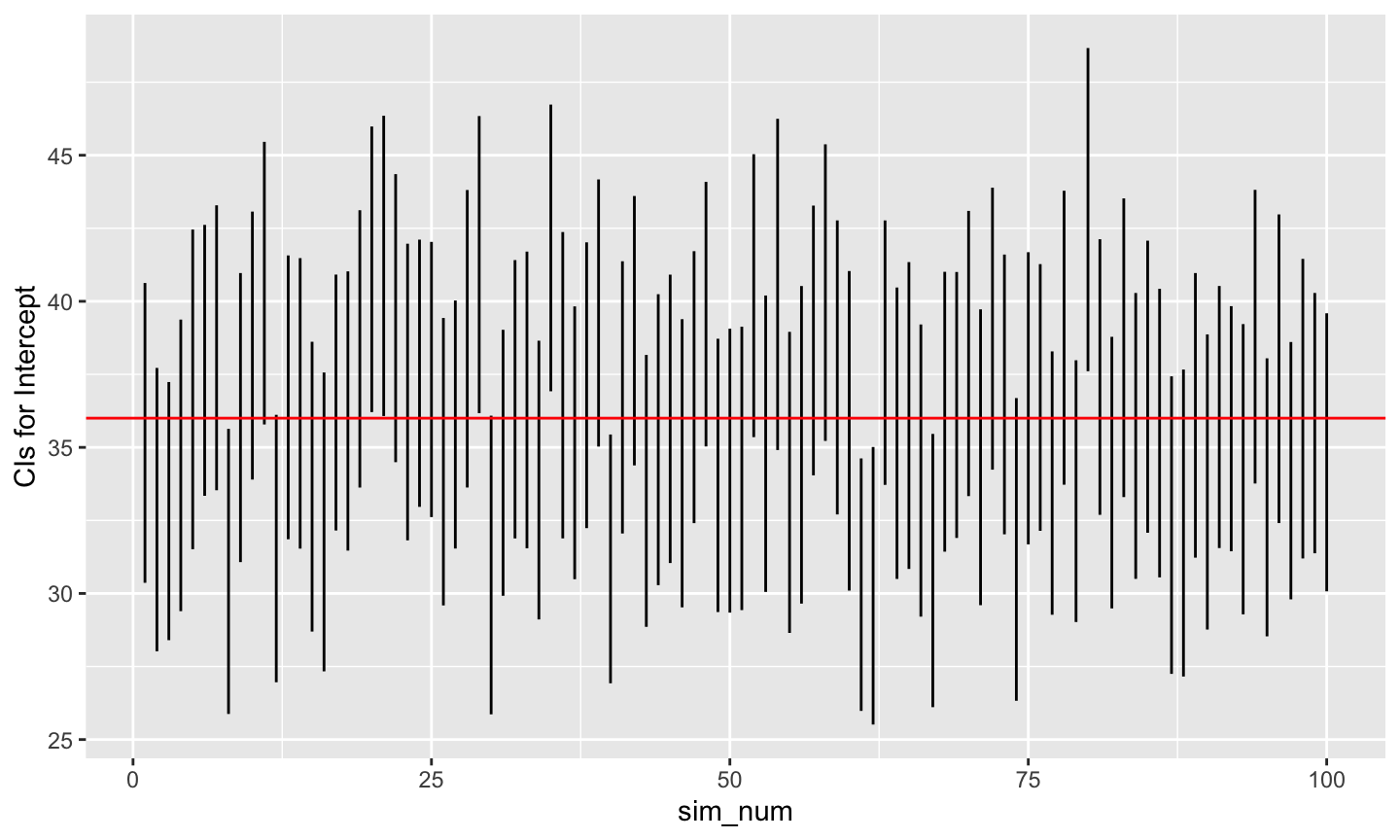
# Plot beta0 min and max (now called V3, V4)
ggplot(data = ht_wt_sims) +
  aes(x = sim_num) +
  geom_linerange(mapping = aes(ymin = beta0.lo,
                                ymax = beta0.hi)) +
  ylab("CIs for Intercept") +
  geom_hline(yintercept = beta0, color = "red")

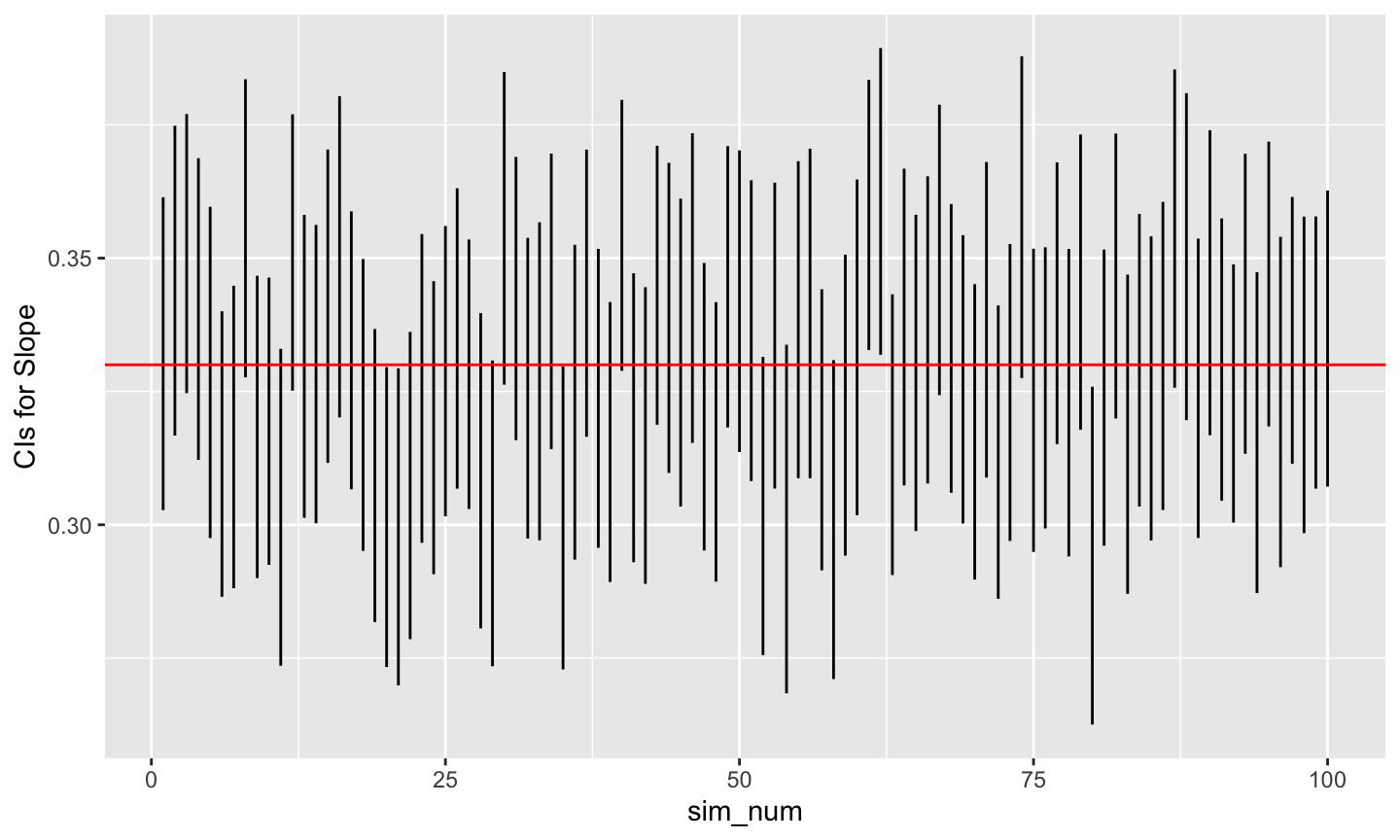
# Plot beta1 min and max (now called V5, V6)
ggplot(data = ht_wt_sims) +
  aes(x = sim_num) +
  geom_linerange(mapping = aes(ymin = beta1.lo,
                                ymax = beta1.hi)) +
  ylab("CIs for Slope") +
  geom_hline(yintercept = beta1, color = "red")

How about a factorial design?

# Simulation parameters
n_subs = 30
trials_per_cond = 100

letters_numbers_rt_diff = 50 # ms
rt_mean_across_subs = 350
sigma = 50
cond_labels = c("letter", "number")
cond_rts <- c("letter" = 0, "number" = letters_numbers_rt_diff)

stim_types <- factor(x = rep(x = c(1,2), 
                             trials_per_cond), 
                     labels = cond_labels)

#sample(factor(x=rep(c("letter", "number"), 100)), 200)
random_stim_types <- sample(stim_types, trials_per_cond*length(cond_labels))

mean_sub_rt <- rnorm(n = 1, mean = rt_mean_across_subs, sd = sigma)
trial_rt <- array(0, dim = length(random_stim_types))

# Generate RTs based on trial, condition
for (t in 1:length(random_stim_types)) {
  trial_rt[t] <- mean_sub_rt + cond_rts[random_stim_types[t]] + 
    rnorm(n = 1, mean = 0, sd = sigma)
}

# Make data frame
letter_number_df <- data.frame(trial = 1:length(random_stim_types), 
                               stim = random_stim_types, 
                               rt = trial_rt)

letter_number_df %>%
  ggplot(.) +
  aes(x = random_stim_types, y = rt) +
  geom_boxplot() +
  geom_point(alpha = .2)

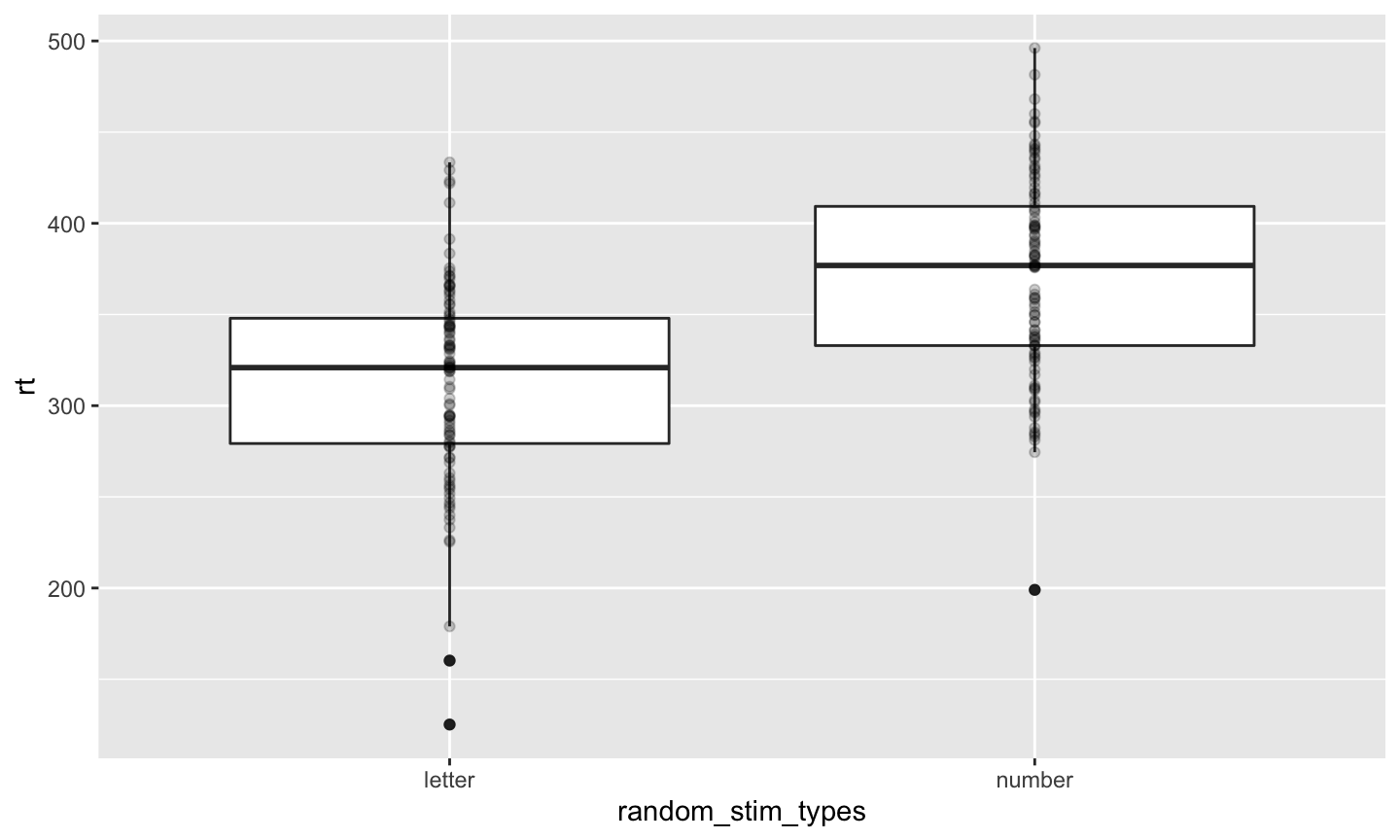
Put this in a function

simulate_sub_rt <- function(trials_per_cond = 100,
                            letters_numbers_rt_diff = 50,
                            rt_mean_across_subs = 350, 
                            sigma = 50) {
  
  cond_rts <- c("letter" = 0, 
                "number" = letters_numbers_rt_diff)
  stim_types <- factor(x = rep(x = c(1,2),
                               trials_per_cond), 
                       labels = c("letter", "number"))
  random_stim_types <- sample(stim_types, 2*trials_per_cond)

  mean_sub_rt <- rnorm(n = 1, 
                       mean = rt_mean_across_subs, 
                       sd = sigma)
  trial_rt <- array(0, dim = length(random_stim_types))

  # Generate RTs based on trial, condition
  for (t in 1:length(random_stim_types)) {
    trial_rt[t] <- mean_sub_rt + cond_rts[random_stim_types[t]] +
      rnorm(n = 1, mean = 0, sd = sigma)
    }

  # Make data frame
  letter.number.df <- data.frame(trial = 1:length(random_stim_types), 
                                 stim = random_stim_types, 
                                 rt = trial_rt)
}

Create code to a set of participants and create one merged data frame

make_sub_rt_df <- function(sub.id) {
  sub_rt_df <- simulate_sub_rt()
  sub_rt_df$sub.id <- sub.id
  sub_rt_df
}

# Use lapply to make separate data frames for all subs
sub_rt_df_list <- lapply(1:n_subs, make_sub_rt_df)

# Use Reduce() with the merge function to make one big file
sub_rt_df_merged <- Reduce(function(x, y) merge(x, y, all=TRUE), sub_rt_df_list)

Now, want to see what we have?

ggplot(data = sub_rt_df_merged) +
  aes(x=stim, y=rt, color=stim) +
  geom_boxplot() +
  facet_grid(facets = . ~ as.factor(sub.id)) +
  theme(axis.text.x.bottom = element_blank(),
        axis.ticks.x.bottom = element_blank())

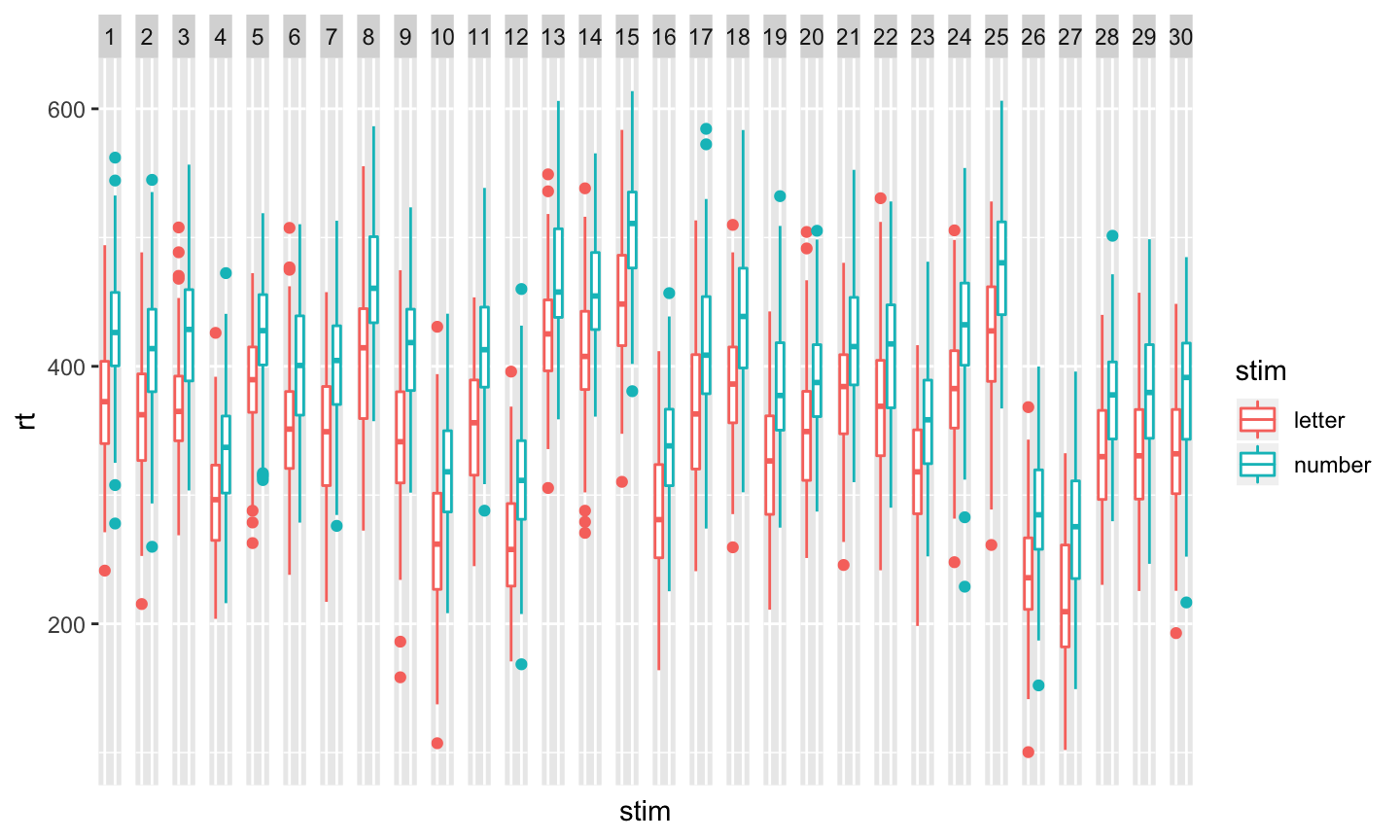
And, just for fun

library(lme4)
fit1 <- lmer(formula = rt ~ stim + (1|sub.id), data = sub_rt_df_merged)
summary(fit1)
## Linear mixed model fit by REML ['lmerMod']
## Formula: rt ~ stim + (1 | sub.id)
##    Data: sub_rt_df_merged
## 
## REML criterion at convergence: 64209.2
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -4.0626 -0.6703  0.0011  0.6620  3.3775 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  sub.id   (Intercept) 3081     55.51   
##  Residual             2535     50.35   
## Number of obs: 6000, groups:  sub.id, 30
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)   347.26      10.18   34.13
## stimnumber     50.62       1.30   38.94
## 
## Correlation of Fixed Effects:
##            (Intr)
## stimnumber -0.064

Or

fit2 <- aov(formula = rt ~ stim + Error(as.factor(sub.id)), data = sub_rt_df_merged)
summary(fit2)
## 
## Error: as.factor(sub.id)
##           Df   Sum Sq Mean Sq F value Pr(>F)
## Residuals 29 17943263  618733               
## 
## Error: Within
##             Df   Sum Sq Mean Sq F value Pr(>F)    
## stim         1  3843699 3843699    1516 <2e-16 ***
## Residuals 5969 15131695    2535                   
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Next time

  • Doing other useful things with R and R Markdown

Resources

Software

This talk was produced on 2020-02-27 in RStudio using R Markdown. The code and materials used to generate the slides may be found at https://github.com/psu-psychology/psy-525-reproducible-research-2020. Information about the R Session that produced the code is as follows:

## R version 3.6.2 (2019-12-12)
## Platform: x86_64-apple-darwin15.6.0 (64-bit)
## Running under: macOS Mojave 10.14.6
## 
## Matrix products: default
## BLAS:   /System/Library/Frameworks/Accelerate.framework/Versions/A/Frameworks/vecLib.framework/Versions/A/libBLAS.dylib
## LAPACK: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRlapack.dylib
## 
## locale:
## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
## 
## attached base packages:
## [1] stats     graphics  grDevices utils     datasets 
## [6] methods   base     
## 
## other attached packages:
## [1] lme4_1.1-21     Matrix_1.2-18   gapminder_0.3.0
## [4] dplyr_0.8.4     ggplot2_3.2.1  
## 
## loaded via a namespace (and not attached):
##  [1] Rcpp_1.0.3         nloptr_1.2.1      
##  [3] plyr_1.8.5         pillar_1.4.3      
##  [5] compiler_3.6.2     tools_3.6.2       
##  [7] boot_1.3-23        digest_0.6.25     
##  [9] packrat_0.5.0      nlme_3.1-142      
## [11] lattice_0.20-38    evaluate_0.14     
## [13] lifecycle_0.1.0    tibble_2.1.3      
## [15] gtable_0.3.0       pkgconfig_2.0.3   
## [17] rlang_0.4.4        yaml_2.2.1        
## [19] xfun_0.12          withr_2.1.2       
## [21] stringr_1.4.0      knitr_1.28        
## [23] grid_3.6.2         tidyselect_1.0.0  
## [25] tufte_0.5          glue_1.3.1        
## [27] R6_2.4.1           databraryapi_0.1.9
## [29] rmarkdown_2.1      minqa_1.2.4       
## [31] purrr_0.3.3        farver_2.0.3      
## [33] reshape2_1.4.3     magrittr_1.5      
## [35] MASS_7.3-51.5      splines_3.6.2     
## [37] scales_1.1.0       htmltools_0.4.0   
## [39] assertthat_0.2.1   colorspace_1.4-1  
## [41] labeling_0.3       stringi_1.4.6     
## [43] lazyeval_0.2.2     munsell_0.5.0     
## [45] crayon_1.3.4

References