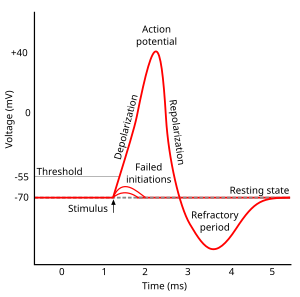
- Another take on the resting and action potentials
- Action potential propagation
- (if time) Wherefore brains?
- Review for Exam 1
2019-02-06 11:48:50
Today's Topics
Another take…
The Hodgkin-Huxley (HH) model

By Krishnavedala -
Own work, CC0, Link
HH model: Membrane as simple circuit
- Membrane as capacitor (C): stores charge
- Ion channels: resistors that can vary in conductance (\(g=\frac{1}{R}\))
- Ion flows create current (I)
- Ohms Law: \(V=\frac{I}{g}\) or \(Vg=I\)
The \(K^+\) story
- \(Na^+\)/\(K^+\) pump pulls \(K^+\) in
- \([K^+]_{in}\) (~150 mM) >> \([K^+]_{out}\) (~4 mM)
- Outward flow of \(K^+\) through passive/leak channels
- Outflow stops when membrane potential, \(V_m\) = equilibrium potential for \(K^+\)
Equilibrium potential
- Voltage (\(V_{K}\)) that keeps system in equilibrium
- \([K^+]_{in}\) >> \([K^+]_{out}\)
- Nernst equation
- \(V_{K}\) = \(\frac{RT}{(+1)F}ln(\frac{[K^+]_{out}}{[K^+]_{in}})\)
- \(V_{K}\) = ~ -90 mV
- Negative in/positive out keeps in/out concentration gradient
Equilibrium potential
- \(K^+\) flows out through passive/leak channels
- Most \(K^+\) remains near membrane
- Separation from \(A^-\) creates charge \(\frac{K+K+K+K+K+}{A-A-A-A-A-}\) along capacitor-like membrane
- \(V_m\) (membrane potential) –> \(V_{K^+}\)
Equilibrium potentials calculated under typical conditions
| Ion | [inside] | [outside] | Voltage |
|---|---|---|---|
| K+ | ~150 mM | ~4 mM | ~ -90 mV |
| Na+ | ~10 mM | ~140 mM | ~ +55-60 mV |
| Cl- | ~10 mM | ~110 mM | ~ - 65-80 mV |
The \(Na^+\) story
- \(Na^+\)/\(K^+\) pump pushes \(Na^+\) out
- \([Na^+]_{in}\) (~10 mM) << \([Na^+]_{out}\) (~140 mM)
- Equilibrium potential for \(Na^+\), \(V_{Na^+}\) = ~ +55 mV
- Inside positive/outside negative to maintain outside > inside concentration gradient
- If \(Na^+\) alone, \(V_m\) –> \(V_{Na}\) (~ +55 mV)
Resting potential
- Sum of outward \(K^+\) and inward \(Na^+\)
- Membrane more permeable to \(K^+\) than \(Na^+\), \(p_{K+}> p_{Na^+}\)
- Outward flow of \(K^+\) > inward flow of \(Na^+\)
- Resting potential (~-70 mV) closer to \(Ve_{K}\) (-90 mV) than \(Ve_{Na}\) (+55 mV)
Resting potential
- Goldman-Hodgkin-Katz equation
- \(V_m = \frac{RT}{F}ln(\frac{p_{K}[K^+]_{out}+p_{Na}[Na^+]_{out}}{p_{K}[K^+]_{in}+p_{Na}[Na^+]_{in}})\)
"Driving force" and equilibrium potential
- "Driving Force" on a given ion depends on difference between
- Equilibrium potential for given ion AND
- Neuron's current membrane potential (\(V_m\))
- \(V_m\) reflects combined effects of all ions
"Driving force" and equilibrium potential
- Anthropomorphic metaphor
- \(K^+\) "wants" to flow out (hyperpolarize neuron)
- \(Na^+\) "wants" to flow in (depolarize neuron)
- Strength of that "desire" depends on distance from equilibrium potential
Action potentials and driving forces

Voltage-gated \(Na^+\) and \(K^+\) channels
- Dynamic elements; change state over time
- HH equations describe state changes
- Open and close with changes in voltage
- Voltage-gated \(Na^+\) also inactivate; de-inactivate as voltage changes
Neuron at rest
- Driving force on \(K^+\) weakly out
- -70 mV - (-90 mV) = +20 mV
- Driving force on \(Na^+\) strongly in
- -70 mV - (+55 mV) = -125 mV
- \(Na^+\)/\(K^+\) pump maintains concentrations

Action potential rising phase
- Voltage-gated \(Na^+\) channels open
- Membrane permeability to \(Na^+\) increases
- \(Na^+\) inflow through passive + voltage-gated channels
- continued \(K^+\) outflow through passive channels

Peak
- Membrane permeability to \(Na^+\) reverts to resting state
- Voltage-gated \(Na^+\) channels close & inactivate
- Slow inflow due to small driving force (+30 mV - 55mV = -25 mv)
Peak
- Membrane permeability to \(K^+\) increases
- Voltage-gated \(K^+\) channels open
- Fast outflow due to strong driving force (+30 mv - (-90 mv) = +120 mV)

Falling phase
- \(K^+\) outflow
- Through voltage-gated \(K^+\) and passive \(K^+\) channels
- \(Na^+\) inflow
- Through passive channels only

Absolute refractory phase
- Cannot generate action potential (AP) no matter the size of the stimulus
- Membrane potential more negative (-90 mV) than at rest (-70 mV)
- Voltage-gated \(Na^+\) channels still inactivated
- Driving force on \(Na^2\) high (-90 mv - 55 mV = -145 mV), but too bad
- Voltage-gated \(K^+\) channels closing
- Driving force on \(K^+\) tiny or absent
- \(Na^2\)/\(K^2\) pump restoring concentration balance

Relative refractory period
- Can generate AP with larg(er) stimulus
- Some voltage-gated \(Na^+\) 'de-inactivate', can open if
- Larger input
- Membrane potential is more negative than resting potential

Neuron at rest
- Voltage-gated \(Na^+\) closed, but ready to open
- Voltage-gated \(K^+\) channels closed, but ready to open
- Membrane potential \(V_m\) at rest (~60-75 mV)
- \(Na^+\)/\(K^+\) pump still working…

| Phase | Ion | Driving force | Flow direction | Flow magnitude |
|---|---|---|---|---|
| Rest | K+ | 20 mV | out | small |
| Na+ | 125 mV | in | small |

| Phase | Ion | Driving force | Flow direction | Flow magnitude |
|---|---|---|---|---|
| Rising | K+ | growing | out | growing |
| Na+ | shrinking | in | high |

| Phase | Ion | Driving force | Flow direction | Flow magnitude |
|---|---|---|---|---|
| Peak | K+ | 120 mV | out | high |
| Na+ | 20 mV | out | small |

| Phase | Ion | Driving force | Flow direction | Flow magnitude |
|---|---|---|---|---|
| Falling | K | shrinking | out | high |
| Na+ | growing | in | small |

| Phase | Ion | Driving force | Flow direction | Flow magnitude |
|---|---|---|---|---|
| Refractory | K | ~0 mV | out | small |
| Na+ | 145 mV | in | small |
Animation
Generating APs
- Axon hillock
- Portion of soma adjacent to axon
- Integrates/sums input to soma
- Axon initial segment
- Umyelinated portion of axon adjacent to soma
- Voltage-gated Na+ and K+ channels exposed
- If sum of input to soma > threshold, voltage-gated Na+ channels open
Axon hillock, axon initial segment

Axon Hillock" by M.aljar3i - Own work. Licensed under CC BY-SA 3.0 via Commons
AP propagation
- Propagation
- move down axon, away from soma, toward axon terminals.
- Unmyelinated axon
- Each segment "excites" the next
AP propagation is like
AP propagation
- Myelinated axon
- AP "jumps" between Nodes of Ranvier via saltatory conduction
- Nodes of Ranvier == unmyelinated sections of axon
- voltage-gated \(Na^+\), \(K_+\) channels exposed
- Current flows through myelinated segments
Question
- Why does AP flow in one direction, away from soma?
- Soma does not have (many) voltage-gated \(Na^+\) channels.
- Soma is not myelinated.
- Refractory periods mean polarization only in one direction.
Question
- Why does AP flow in one direction, away from soma?
- Soma does not have (many) voltage-gated \(Na^+\) channels.
- Soma is not myelinated.
- Refractory periods mean polarization only in one direction.
Conduction velocities
Information processing
- AP amplitudes don't vary (much)
- All or none
- \(Na^+\)/\(K^+\) pumps working all the time
- \([K^+]\) & \([Na^+]\) don't vary much, so
- \(V_{K^+}\) & \(V_{Na^+}\) don't vary much
- AP frequency and timing vary
- Rate vs. timing codes
- Neurons use both
Wherefore brains?
Why brains?
Escherichia Coli (E. Coli)
- Tiny, single-celled bacterium
- Feeds on glucose
- Chemo ("taste") receptors on surface membrane
- Flagellum for movement
- Food concentration regulates duration of "move" phase
- ~4 ms for chemical signal to diffuse from anterior/posterior
Paramecium
- 300K larger than E. Coli
- Propulsion through coordinated beating of cilia
- Diffusion from head to tail ~40 s!
- Use electrical signaling instead
- Na+ channel opens (e.g., when stretched)
- Voltage-gated Ca++ channels open, Ca++ enters, triggers cilia
- Voltage propagates across cell within ms
Caenorhabditis Elegans (C. Elegans)
- ~10x larger than paramecium
- multi-cellular (\(n\)=959)
- \(n=302\) are neurons & \(n=56\) are glia
- Can swim, forage, mate
Why brains?
- Bigger bodies (need to send specific info)
- For neurons (point to point communication)
- Live longer
- Do more, do it faster
Next time…
- Exam 1