- Warm-up
- What good are brains?
- Action potential propagation
- Another take on the resting and action potentials
2022-02-15 08:10:21
Today’s Topics
Warm-up
Which force(s) act to move Na+ ions inward in a neuron at resting potential?
A. The force of diffusion B. The dark side of the force C. The electrostatic force D. Gravity E. Both A. and C.
Which force(s) act to move Na+ ions inward in a neuron at resting potential?
A. The force of diffusion B. The dark side of the force C. The electrostatic force D. Gravity E.
Both A. and C.
At the (positive voltage) peak of the action potential, which force(s) act to move K+ ions outward?
A. The force of diffusion B. The dark side of the force C. The electrostatic force D. Gravity E. Both A. and C.
At the (positive voltage) peak of the action potential, which force(s) act to move K+ ions outward?
A. The force of diffusion B. The dark side of the force C. The electrostatic force D. Gravity E.
Both A. and C.
What good are brains?
Why brains?
Escherichia Coli (E. Coli)
- Tiny, single-celled bacterium
- Feeds on glucose
- Chemosensory (“taste”) receptors on surface membrane
- Flagellum for movement
- Food concentration regulates duration of “move” phase
- ~4 ms for chemical signal to diffuse from anterior/posterior
Paramecium
- 300K larger than E. Coli
- Propulsion through coordinated beating of cilia
- Diffusion from head to tail ~40 s!
- Use electrical signaling instead
- \(Na^+\) channel opens (e.g., when stretched)
- Voltage-gated \(Ca^{++}\) channels open, \(Ca^{++}\) enters, triggers cilia movement
- Voltage propagates along cell membrane within ms
Caenorhabditis Elegans (C. Elegans)
- ~\(10x\) larger than paramecium
- multi-cellular (\(n=959\) cells total)
- \(n=302\) are neurons & \(n=56\) are glia
- nervous system 37% of cells vs. ~0.5% in humans
- Can swim, forage, mate
Why brains?
- Bigger bodies (need to process specific info, move through water, air, on land)
- For neurons (point to point communication)
- Live longer
- Do more, do it faster, over larger distances & longer time periods
Why chemical & electrical communication?
- Chemical communication : short distances
- Cheap, energy-efficient, “compute with chemistry”
- Electrical communication : long distances
- More “expensive”/less energy-efficient
How action potentials propagate
Axon is like an electrical cable
knitr::include_graphics("http://pittmedneuro.com/img/Cable.jpg")
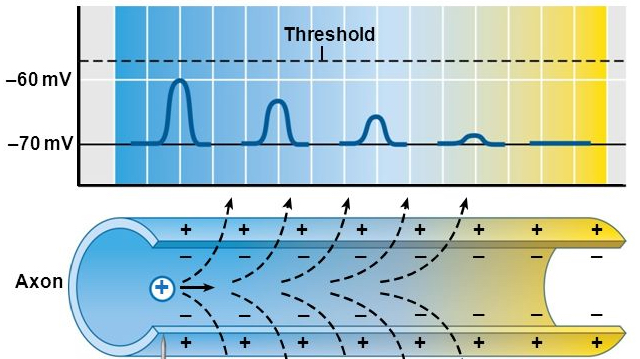
AP propagation
- Propagation
- move down axon, away from soma, toward axon terminals.
- Unmyelinated axon
- Each segment “excites” the next
AP propagation is like
AP propagation
- Myelinated axon
- AP “jumps” between Nodes of Ranvier via saltatory conduction
- Nodes of Ranvier == unmyelinated sections of axon
- voltage-gated \(Na^+\), \(K^+\) channels exposed
- Current flows through myelinated segments
Question
- Why does AP flow in one direction, away from soma?
- Soma does not have (many) voltage-gated \(Na^+\) channels.
- Soma is not myelinated.
- Refractory periods mean polarization only in one direction.
Question
- Why does AP flow in one direction, away from soma?
- Soma does not have (many) voltage-gated \(Na^+\) channels.
- Soma is not myelinated.
- Refractory periods mean polarization only in one direction.
Conduction velocities
Conduction velocities
- Axons carry information at different rates
- More myelin -> faster
- Larger diameter axon -> faster
- PNS seems to prioritize
- Somatosensory information & muscle control
Information processing
- AP amplitudes don’t vary (much)
- All or none
- \(Na^+\)/\(K^+\) pumps working all the time
- \([K^+]\) & \([Na^+]\) don’t vary much, so
- \(V_{K^+}\) & \(V_{Na^+}\) don’t vary much
- AP frequency and timing vary
- Rate vs. timing codes
- Neurons use both
Another take…
The Hodgkin-Huxley (HH) model

By Krishnavedala -
Own work, CC0, Link
HH model: Membrane as simple circuit
- Membrane as capacitor (C): stores charge
- Ion channels: resistors that can vary in conductance (\(g=\frac{1}{R}\))
- Ion flows create current (I)
- Ohms Law: \(V=\frac{I}{g}\) or \(Vg=I\)
The \(K^+\) story
- \(Na^+\)/\(K^+\) pump pulls \(K^+\) in
- \([K^+]_{in}\) (~150 mM) >> \([K^+]_{out}\) (~4 mM)
- Outward flow of \(K^+\) through passive/leak channels via force of diffusion
- Outflow stops when membrane potential, \(V_m\) = equilibrium potential for \(K^+\)
Equilibrium potential
- Voltage (\(V_{K}\)) that keeps system in equilibrium
- \([K^+]_{in}\) >> \([K^+]_{out}\)
- Nernst equation
- \(V_{K}\) = \(\frac{RT}{(+1)F}ln(\frac{[K^+]_{out}}{[K^+]_{in}})\)
- \(V_{K}\) = ~ -90 mV
- Negative inside/positive outside keeps \([K^+]\) concentration gradient
Equilibrium potential
- \(K^+\) flows out through passive/leak channels
- Most \(K^+\) remains near membrane
- Separation from \(A^-\) creates charge \(\frac{K+K+K+K+K+}{A-A-A-A-A-}\) along capacitor-like membrane
- \(V_m\) (membrane potential) –> \(V_{K^+}\)
Equilibrium potentials calculated under typical conditions
| Ion | [inside] | [outside] | Voltage |
|---|---|---|---|
| K+ | ~150 mM | ~4 mM | ~ -90 mV |
| Na+ | ~10 mM | ~140 mM | ~ +55-60 mV |
| Cl- | ~10 mM | ~110 mM | ~ - 65-80 mV |
The \(Na^+\) story
- \(Na^+\)/\(K^+\) pump pushes \(Na^+\) out
- \([Na^+]_{in}\) (~10 mM) << \([Na^+]_{out}\) (~140 mM)
- Equilibrium potential for \(Na^+\), \(V_{Na^+}\) = ~ +55 mV
- Inside positive/outside negative to \([Na^+]\) concentration gradient
- If \(Na^+\) alone, \(V_m\) –> \(V_{Na}\) (~ +55 mV)
Resting potential
- Sum of outward \(K^+\) and inward \(Na^+\)
- Membrane more permeable to \(K^+\) than \(Na^+\), \(p_{K+}> p_{Na^+}\)
- Outward flow of \(K^+\) > inward flow of \(Na^+\)
- Resting potential (~-70 mV) closer to \(V_{K^+}\) (-90 mV) than \(V_{Na^+}\) (+55 mV)
Resting potential
- Goldman-Hodgkin-Katz equation
- \(V_m = \frac{RT}{F}ln(\frac{p_{K}[K^+]_{out}+p_{Na}[Na^+]_{out}}{p_{K}[K^+]_{in}+p_{Na}[Na^+]_{in}})\)
“Driving force” and equilibrium potential
- “Driving Force” on a given ion depends on difference between
- Equilibrium potential for given ion AND
- Neuron’s current membrane potential (\(V_m\))
- \(V_m\) reflects combined effects of all ions
“Driving force” and equilibrium potential
- Anthropomorphic (‘in human form’) metaphor
- \(K^+\) “wants” to flow out (hyperpolarize neuron)
- \(Na^+\) “wants” to flow in (depolarize neuron)
- Strength of that “desire” depends on distance from the equilibrium potential for each ion
- Humans (often) think about causes and effects in psychological terms
- Ok to do so, as long as we recognize when it’s just a metaphor
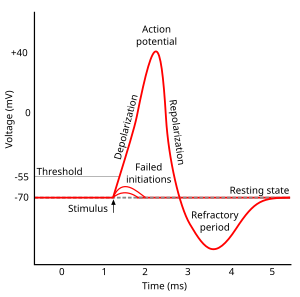
Action potentials and driving forces

Voltage-gated \(Na^+\) and \(K^+\) channels
- Dynamic elements; change state over time
- Hodgkin-Huxley (HH) equations describe state changes
- Open and close with changes in voltage
- Voltage-gated \(Na^+\) also inactivate; de-inactivate as voltage changes
Neuron at rest
- Driving force on \(K^+\) weakly out
- -70 mV - (-90 mV) = +20 mV
- Driving force on \(Na^+\) strongly in
- -70 mV - (+55 mV) = -125 mV
- \(Na^+\)/\(K^+\) pump maintains concentrations

Action potential rising phase
- Voltage-gated \(Na^+\) channels open
- Membrane permeability to \(Na^+\) increases
- \(Na^+\) inflow through passive + voltage-gated channels
- continued \(K^+\) outflow through passive channels

Peak
- Membrane permeability to \(Na^+\) reverts to resting state
- Voltage-gated \(Na^+\) channels close & inactivate
- Slow inflow due to small driving force (+30 mV - 55mV = -25 mv)
Peak
- Membrane permeability to \(K^+\) increases
- Voltage-gated \(K^+\) channels open
- Fast outflow due to strong driving force (+30 mv - (-90 mv) = +120 mV)

Falling phase
- \(K^+\) outflow
- Through voltage-gated \(K^+\) and passive \(K^+\) channels
- \(Na^+\) inflow
- Through passive channels only

Absolute refractory phase (period)
- Cannot generate action potential (AP) no matter the size of the stimulus
- Membrane potential more negative (~-90 mV) than at rest (~-70 mV)
- Voltage-gated \(Na^+\) channels still inactivated
- Driving force on \(Na^+\) high (-90 mv - 55 mV = -145 mV), but…
Absolute refractory phase (period)
- Voltage-gated \(K^+\) channels closing
- Driving force on \(K^+\) tiny or absent
- \(Na^+\)/\(K^+\) pump restoring concentration balance

Relative refractory phase (period)
- Can generate AP with larg(er) stimulus
- Some voltage-gated \(Na^+\) ‘de-inactivate’, can open if
- Larger input
- Membrane potential is more negative than resting potential

Neuron at rest
- Voltage-gated \(Na^+\) closed, but ready to open
- Voltage-gated \(K^+\) channels closed, but ready to open
- Membrane potential \(V_m\) at rest (~60-75 mV)
- \(Na^+\)/\(K^+\) pump still working…

| Phase | Ion | Driving force | Flow direction | Flow magnitude |
|---|---|---|---|---|
| Rest | K+ | 20 mV | out | small |
| Na+ | 125 mV | in | small |

| Phase | Ion | Driving force | Flow direction | Flow magnitude |
|---|---|---|---|---|
| Rising | K+ | growing | out | growing |
| Na+ | shrinking | in | high |

| Phase | Ion | Driving force | Flow direction | Flow magnitude |
|---|---|---|---|---|
| Peak | K+ | 120 mV | out | high |
| Na+ | 20 mV | out | small |

| Phase | Ion | Driving force | Flow direction | Flow magnitude |
|---|---|---|---|---|
| Falling | K | shrinking | out | high |
| Na+ | growing | in | small |

| Phase | Ion | Driving force | Flow direction | Flow magnitude |
|---|---|---|---|---|
| Refractory | K | ~0 mV | out | small |
| Na+ | 145 mV | in | small |
Animation
Generating APs
- Axon hillock
- Portion of soma adjacent to axon
- Integrates/sums input to soma
- Axon initial segment
- Umyelinated portion of axon adjacent to soma
- Voltage-gated \(Na^+\) and \(K^+\) channels exposed
- If sum of input to soma > threshold, voltage-gated \(Na^+\) channels open
Axon hillock, axon initial segment

Axon Hillock” by M.aljar3i - Own work. Licensed under CC BY-SA 3.0 via Commons
Next time…
- Exam 1