Bias

Figure 63: T. Baker (2023)

Kinds of bias

  • Analysts’ prior assumptions
  • Researcher, reviewer, and publication bias toward positive (vs. negative/null) results
    • File-drawer effect
  • Preference for simple results (c.f., Stapel)
  • Overfitting
  • Conflicts of interest
  • p-hacking

Discuss p-hacking exercise

  1. Who got a “significant” result?
  2. How many different analyses did you try?
  3. Who changed their analysis after finding a significant result?
  4. Did anyone try another analysis–after you got a significant result–and keep the non-significant result?

Preparation

It often saves typing to load a set of commands into memory. In R, groups of useful commands are called ‘packages’. We can load a set of useful packages into memory by issuing the following command.

## ── Attaching core tidyverse packages ──────── tidyverse 2.0.0 ──
## ✔ dplyr     1.1.1     ✔ readr     2.1.4
## ✔ forcats   1.0.0     ✔ stringr   1.5.0
## ✔ ggplot2   3.4.2     ✔ tibble    3.2.1
## ✔ lubridate 1.9.2     ✔ tidyr     1.3.0
## ✔ purrr     1.0.1     
## ── Conflicts ────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

If you are interested in a career related to data science, tidyverse is a very powerful set of tools you will want to know more about.

Data entry

Via a Google Sheet: https://docs.google.com/spreadsheets/d/1fnSwFrUcKvgqq_agDLe4t2DHXHtHoOlmLdtLVRSemrI/edit?usp=sharing

Gilmore added data validation (Format/Data Validation) to the columns. Why?

These data are “long”. Each row is a unique observation. Long data are often easier to work with. But not always.

Data gathering

First, I authenticate (sign-in) to Google using my Gmail account. If I haven’t logged in using this script recently, it will ask me to log-in again.

Then I download the Google Sheet to a directory/folder called csv/ using the file name p-hacking.csv.

What does CSV mean?

Why are CSV files often used in data analysis?

Next, I read the CSV file using the read_csv() function.

Functions in R take inputs and deliver outputs. The inputs are file and show_col_types.

The output is an object called p_hacking. It is a table of data that I can refer to with that name.

I like to use the ‘structure’ function or str() to see what the data look like.

Data is a plural noun. So, (when we don’t forget this) we say ‘The data are…’ not ‘The data is…’.

## spc_tbl_ [23 × 16] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
##  $ student           : num [1:23] 0 0 0 1 1 1 2 3 4 4 ...
##  $ analysis          : num [1:23] 1 2 3 1 2 3 1 1 1 2 ...
##  $ party             : chr [1:23] "democrats" "democrats" "democrats" "democrats" ...
##  $ prediction        : chr [1:23] "worse" "worse" "worse" "better" ...
##  $ power_president   : logi [1:23] FALSE FALSE FALSE TRUE TRUE TRUE ...
##  $ power_governors   : logi [1:23] FALSE FALSE FALSE TRUE FALSE TRUE ...
##  $ power_senators    : logi [1:23] TRUE TRUE TRUE TRUE TRUE TRUE ...
##  $ power_reps        : logi [1:23] TRUE TRUE TRUE FALSE FALSE FALSE ...
##  $ econ_employment   : logi [1:23] TRUE TRUE TRUE TRUE TRUE TRUE ...
##  $ econ_inflation    : logi [1:23] FALSE FALSE FALSE FALSE FALSE TRUE ...
##  $ econ_gdp          : logi [1:23] FALSE FALSE FALSE TRUE TRUE TRUE ...
##  $ econ_stocks       : logi [1:23] TRUE TRUE TRUE FALSE FALSE FALSE ...
##  $ factor_in_power   : logi [1:23] FALSE TRUE FALSE TRUE TRUE TRUE ...
##  $ exclude_recessions: logi [1:23] FALSE FALSE TRUE TRUE TRUE TRUE ...
##  $ p_value           : num [1:23] 0.06 0.19 0.02 0.02 0.21 0.32 0.01 0.01 0.18 0.1 ...
##  $ publishable       : chr [1:23] "no" "no" "yes" "yes" ...
##  - attr(*, "spec")=
##   .. cols(
##   ..   student = col_double(),
##   ..   analysis = col_double(),
##   ..   party = col_character(),
##   ..   prediction = col_character(),
##   ..   power_president = col_logical(),
##   ..   power_governors = col_logical(),
##   ..   power_senators = col_logical(),
##   ..   power_reps = col_logical(),
##   ..   econ_employment = col_logical(),
##   ..   econ_inflation = col_logical(),
##   ..   econ_gdp = col_logical(),
##   ..   econ_stocks = col_logical(),
##   ..   factor_in_power = col_logical(),
##   ..   exclude_recessions = col_logical(),
##   ..   p_value = col_double(),
##   ..   publishable = col_character()
##   .. )
##  - attr(*, "problems")=<externalptr>

Questions to explore

Most data analysts find that the process of exploring data is iterative.

We start with a question. That leads to another question. That leads to yet another question.

It is also sometimes cyclical. To answer a question requires that we modify the form of our data file.

I like to start with thinking about “data pictures.” If X was true, what would the data look like?

The following code we may or may not use. I put it here so it’s easier for all of us if we need to make use of it.

Visualize

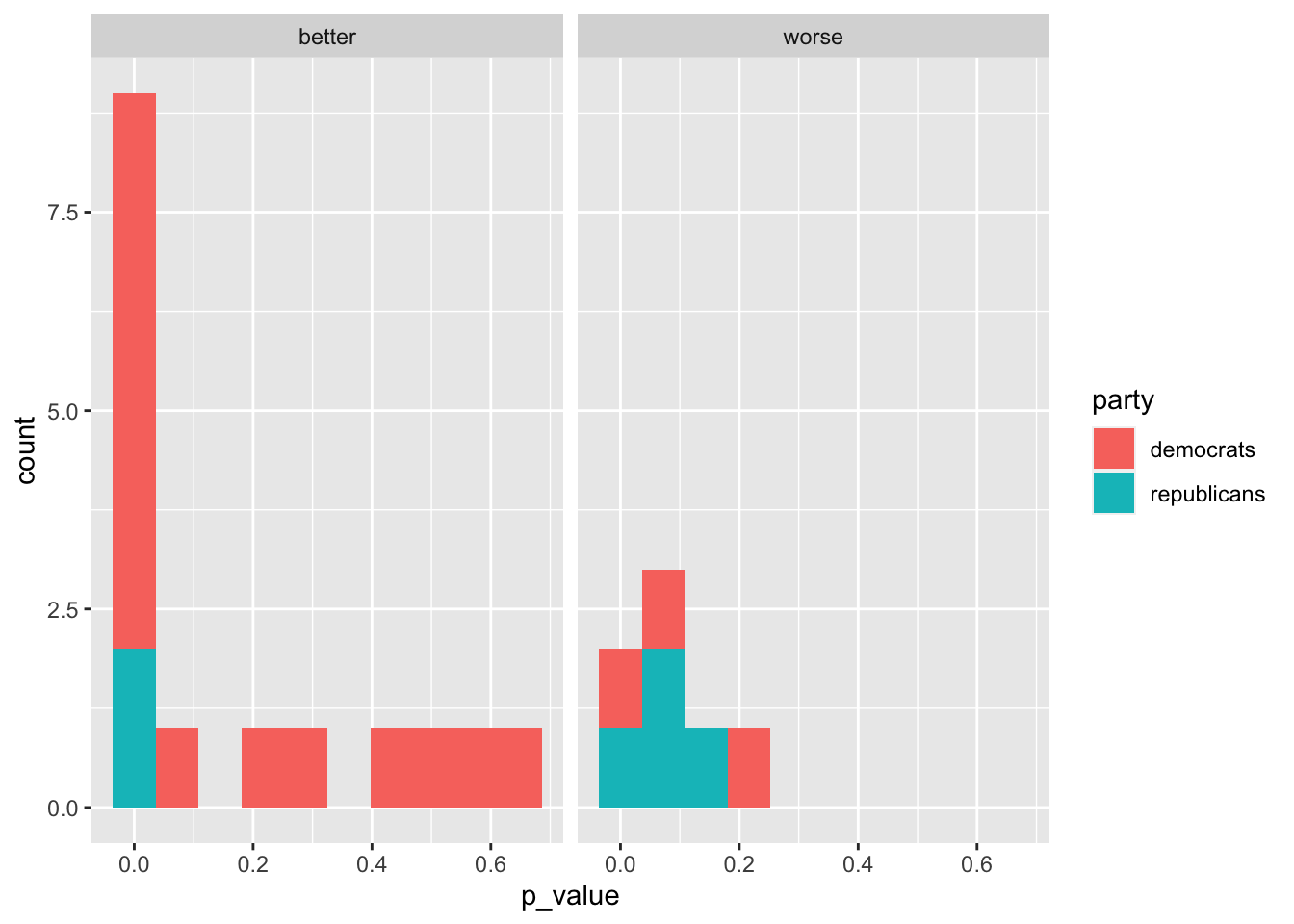
How many different combinations of variable choices are there?

There are \(n=4\) measures of political control; \(n=4\) measures of economic performance; \(n=2\) ‘other’ factors; \(n=2\) prediction choices; and \(n=2\) political parties to focus on.

We can use the combinat package to help us figure this out.

##      [,1]   [,2]  [,3]     [,4]   
## [1,] "pres" "gov" "senate" "house"

This shows us the number of ways we can pick a single political measure from among the 4 choices. We see that there are 4 ways.

The next function shows us the number of ways to pick two measures.

##      [,1]   [,2]     [,3]    [,4]     [,5]    [,6]    
## [1,] "pres" "pres"   "pres"  "gov"    "gov"   "senate"
## [2,] "gov"  "senate" "house" "senate" "house" "house"

There are 6 columns of two, so there must be 6 different ways to pick two measures.

##      [,1]     [,2]    [,3]     [,4]    
## [1,] "pres"   "pres"  "pres"   "gov"   
## [2,] "gov"    "gov"   "senate" "senate"
## [3,] "senate" "house" "house"  "house"

There are 4 different ways to pick 3 measures.

And there is only one way to pick 4 among 4. Make sense?

If we add these up ‘4 + 6 + 4 + 1’ = 15 we get the number of different choices we can make (15) about how many combinations of political power measures are possible.

Since there are also 4 different choices of economic performance measures, we know that there are 15 ways to pick these. Now we can calculate how many different possible combinations of variables there are.

We multiply because each of the choices (political power, economic performance, party, better or worse is independent).

So, there are \(n=\) 1800 of variables we could have chosen. No wonder different students got such different results!

Next time…

References

Baker, T. (2023, February 17). Review found “falsified data” in stanford president’s research, colleagues allege. https://stanforddaily.com/2023/02/17/internal-review-found-falsified-data-in-stanford-presidents-alzheimers-research-colleagues-allege/. Retrieved from https://stanforddaily.com/2023/02/17/internal-review-found-falsified-data-in-stanford-presidents-alzheimers-research-colleagues-allege/
Franco, A., Malhotra, N., & Simonovits, G. (2014). Social science. Publication bias in the social sciences: Unlocking the file drawer. Science, 345(6203), 1502–1505. https://doi.org/10.1126/science.1255484
Ritchie, S. (2020). Science fictions: Exposing fraud, bias, negligence and hype in science (1st ed.). Penguin Random House. Retrieved from https://www.amazon.com/Science-Fictions/dp/1847925669
Rosenthal, R. (1979). The file drawer problem and tolerance for null results. Psychological Bulletin, 86(3), 638–641. https://doi.org/10.1037/0033-2909.86.3.638