Topic 7 Cells of the nervous system
How many cells in the nervous system?
Human vs. non-human cells
- ~ 37 trillion (10^9) (Roy and Conroy 2018) cells
- 10-100 trillion non-human cells (gut, skin/hair, bloodstream, etc.)
- Human bodies are a community
How many neurons and glia?
- Old “lore”: ~100 billion neurons
- New estimate (Azevedo et al. 2009)
- ~86 +/- 8 billion neurons
- ~85 +/- 9 billion glia
- 100-500 trillion synapses, 1 billion/mm^3
How long would it take you to count 170 billion cells?
How would you estimate how long?
- 60 s/min x 60 min/hr x 24 hrs/day x 365 days/ yr = 31,536,000 s/yr
- 1.7e11/31,536,000 = 5,390 years
“Back of the envelope” calculations/guess-timates are extremely useful–in science and in other aspects of life.
Mass of neurons and non-neurons
![[[@azevedo2009equal]](http://doi.org/10.1002/cne.21974)](include/img/azevedo-et-al-fig-1.jpg)
## [1] "tidyverse"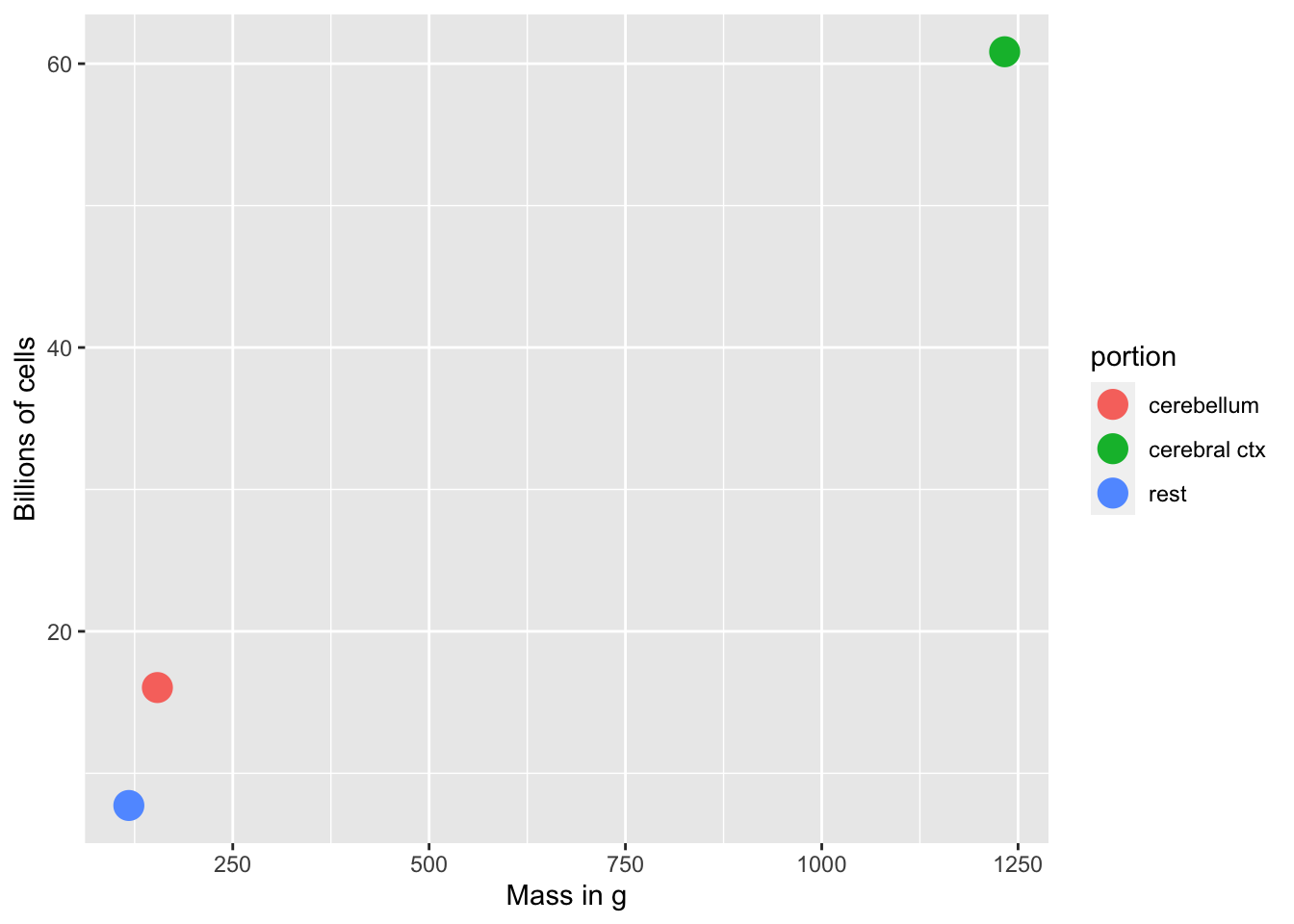
Figure 7.2: Non-neurons: Mass vs. number of cells
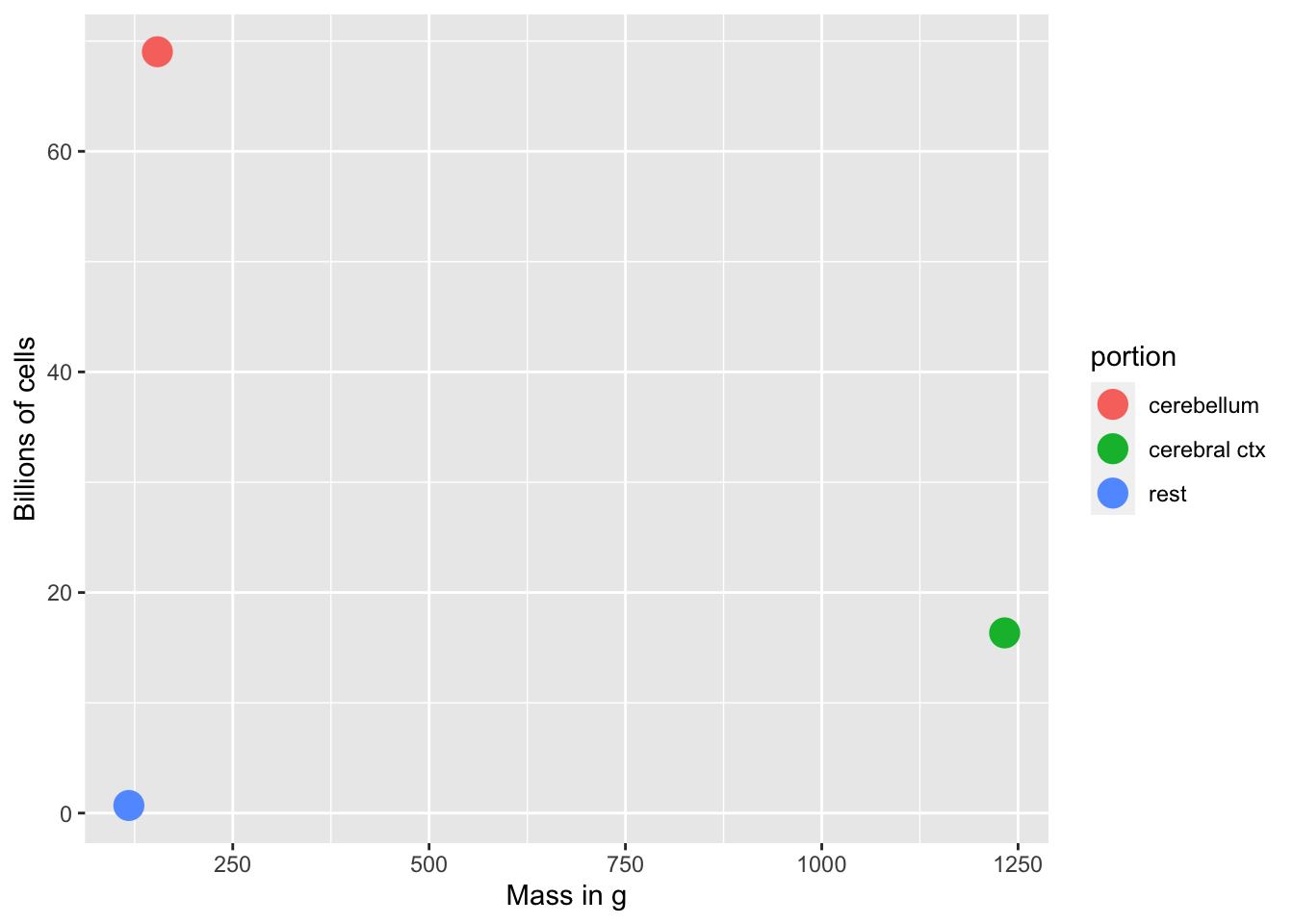
Figure 7.3: Neurons: Mass vs. number of cells
- # of glial cells scales with brain size/mass
- # of neurons doesn’t scale with brain size/mass
- cerebellum small but # of neurons large
“These findings challenge the common view that humans stand out from other primates in their brain composition and indicate that, with regard to numbers of neuronal and nonneuronal cells, the human brain is an isometrically scaled-up primate brain.”
Figure 7.4: The Human Advantage
Glia (neuroglia)
- “Glia” means glue
- Functions
- Structural support
- Metabolic support
- Brain development
- Neural plasticity?
- Multiple types of glial cells
Astrocytes
- “Star-shaped”
- Physical and metabolic support
- Blood/brain barrier
- Regulate concentration of key ions (Ca++/K+) for neural communication
- Regulate concentration of key neurotransmitters (e.g., glutamate)
- Shape brain development, synaptic plasticity
- Regulate local blood flow (part of fMRI’s blood oxygen-dependent BOLD response)
- Regulate/influence communication between neurons, (Bazargani and Attwell 2016)
- Disruption linked to cognitive impairment, disease (Chung et al. 2015)
Figure 7.5: Human astrocyte: Wikipedia
Myelinating cells
- Produce myelin or myelin sheath
- White, fatty substance
- Surrounds many neurons
- The “white” in white matter
- Provide electrical/chemical insulation
- Make neuronal messages faster, less susceptible to noise
Oligodendrocytes
- In brain and spinal cord (Central Nervous System or CNS)
- 1:many neurons
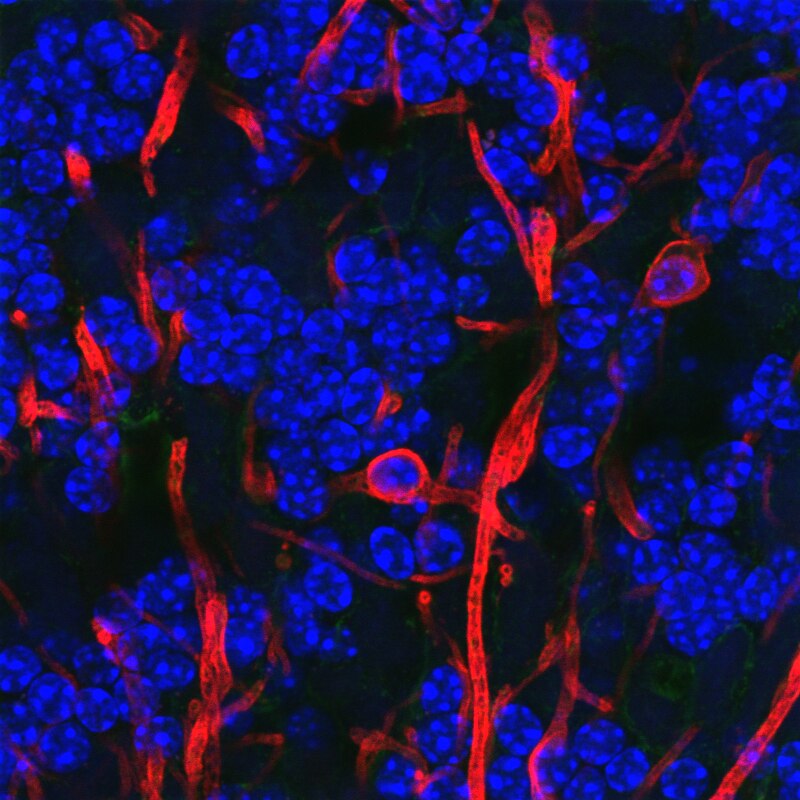
Figure 7.6: Oligodendrocyte: Wikipedia
Schwann cells
- In Peripheral Nervous System (PNS)
- 1:1 neuron
- Facilitate neuro-regeneration
Figure 7.7: Schwann Cell
A (TV-show-inspired) mnemonic for remembering which myelinating glia are found where:
Figure 7.8: Law & Order
Central Oligodendrocytes Peripheral Schwann cells
Figure 7.9: Spock: https://www.syfy.com/sites/syfy/files/styles/blog-post-embedded--tablet/public/2022/05/stangenewworlds_29_spockenviro_jd_3422_v2_fnl_f.jpg
Schwann cells Peripheral Oligodendrocytes Central
Microglia
- Clean-up damaged, dead tissue
- Prune synapses in normal development and disease
- Disruptions in microglia pruning -> impaired functional brain connectivity and social behavior, (Zhan et al. 2014)
Figure 7.10: Microglia (red): http://faculty.sites.uci.edu/kimgreen/bio/microglia-in-the-healthy-brain/
Neurons
Figure 7.11: Neurons in mouse hippocampus: http://www.extremetech.com/wp-content/uploads/2012/03/a-mouse-hippocampus-640x353.jpg
Fun facts about neurons
- Specialized for electrical & chemical communication
- Post-mitotic – don’t divide
- Most born early in life, (Bhardwaj et al. 2006)
- Among longest-lived cells in body, may scale with organism lifespan (Magrassi, Leto, and Rossi 2013)
- Can extend over long distances
Macrostructure of neurons
Figure 7.12: Neuron structure: Wikipedia
Dendrites
- Branch-like “extrusions” from cell body
- Majority of input to neuron
- Cluster close to cell body/soma
- Usually receive info
- Passive (do not regenerate electrical signal) vs. active (regenerate signal)
Figure 7.13: Dendrites: https://i.stack.imgur.com/kfriB.jpg
- Dendritic Spines (protrusions from dendrites)
Figure 7.14: Dendritic spines: https://upload.wikimedia.org/wikipedia/commons/b/b1/Dendritic_spines.jpg
Soma (cell body)
- Varied shapes
- Nucleus
- Chromosomes (genetic material)
- Organelles
- Mitochondria
- Smooth and Rough Endoplasmic reticulum (ER)
Axons
- Another branch-like “extrusion” from soma
- Extend farther than dendrites
- Usually transmit info
- Parts
- Initial segment (closest to soma, unmyelinated)
- Nodes of Ranvier (unmyelinated segments along axon)
- Terminals, axon terminals, terminal buttons, synaptic terminals, synaptic boutons
Synaptic bouton (terminal button)
- Synapse (~5-10K per neuron)
- Presynaptic membrane (sending cell) and postsynaptic (receiving cell) membrane
- Synaptic cleft – space between cells
- Synaptic vesicles
- Pouches of neurotransmitters
- Autoreceptors (detect NTs); transporters (transport NTs across membrane)
Classifying neurons
- Functional role
- Input (sensory), output (motor/secretory), interneurons
- Anatomy of axons
- Unipolar
- Bipolar
- Multipolar
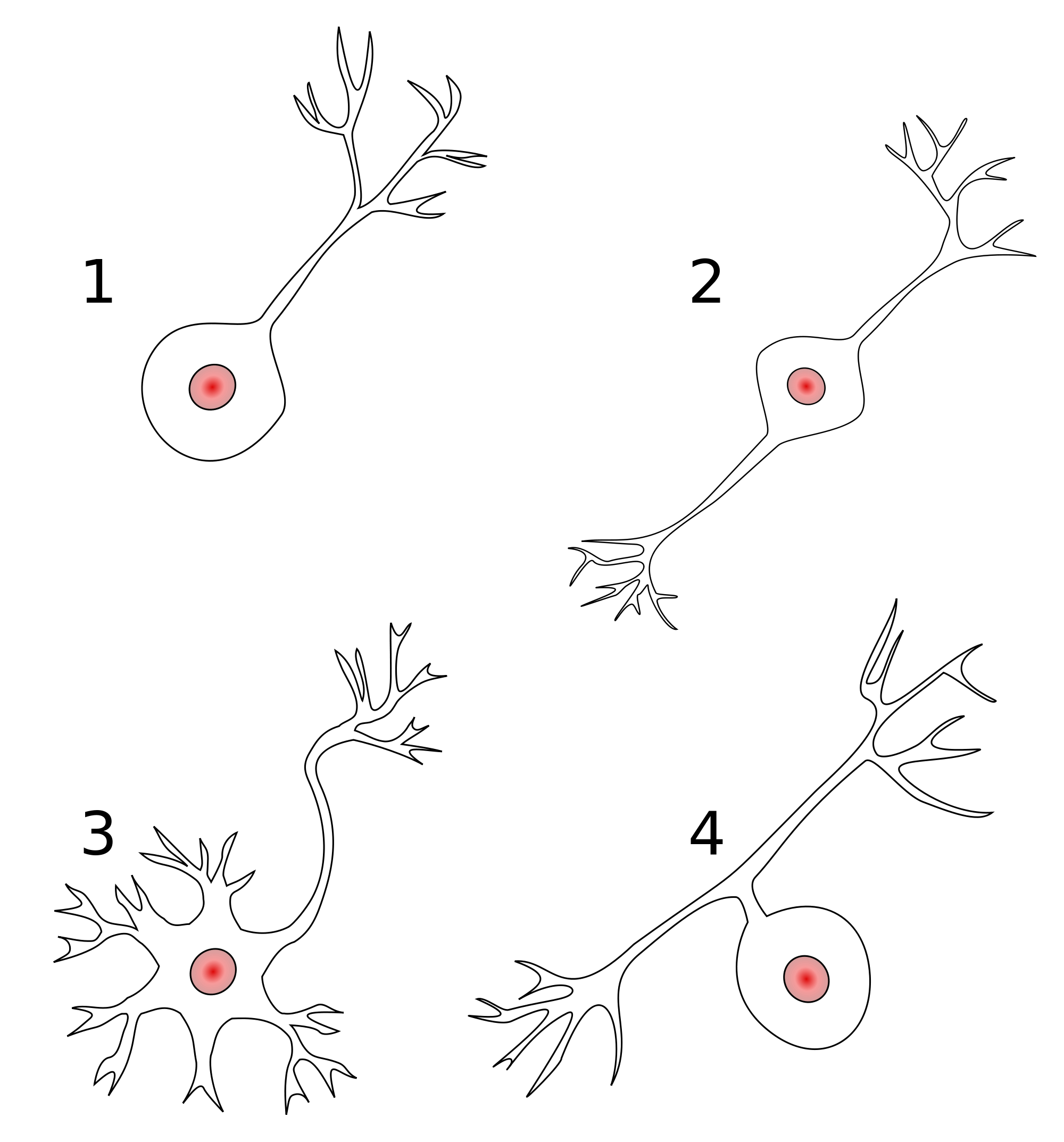
Figure 7.18: Types of neurons: Wikipedia
- By specific anatomy
- Pyramidal cells
- Stellate cells
- Purkinje cells
- Granule cells
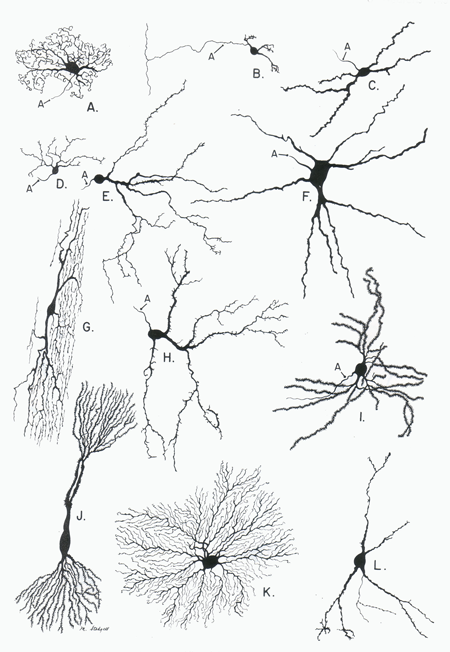
Figure 7.19: Neuronal subtypes: http://biodrawing.com/Neurology_modules/NervousSystemSite/Neuroanatomy/figures/Cytology-Neurons_types_small.png
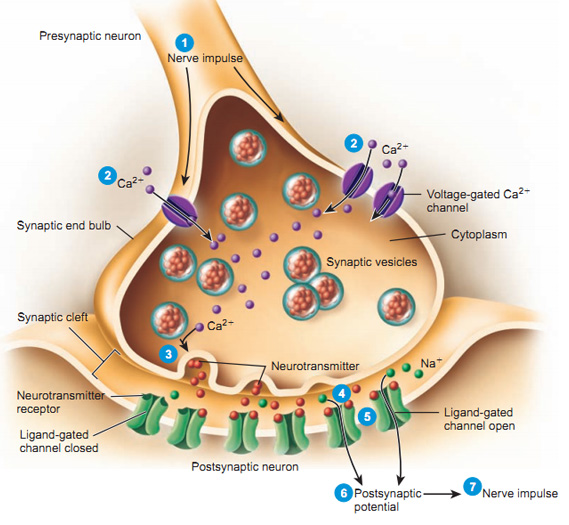
How do neurons communicate?
Types of neural electrical potentials
- Resting potential
- Voltage across neuronal membrane when cell is ‘at-rest’ (not firing)
- Action potential
- Voltage across neuronal membrane when cell is active or firing
Resting potential
- Ions (charged particles)
- Potassium, \(K^+\)
- Sodium, \(Na^+\)
- Chloride, \(Cl^-\)
- Organic anions, \(A^-\)
- Ion channels
- Molecular gateways or doors
- Separation between charges
- Positive and negative charges spatially separated
- A balance of forces
- Force of diffusion
- Electrostatic force
- Forces cause ion flows across membrane
- Force of diffusion consistent (over time)
- Electrostatic force changes
A mnemonic metaphor
- Annie (\(A^-\)) was having a party.
- Used to date Nate (\(Na^+\)), but now sees Karl (\(K^+\))
- Hired bouncers called
- “The Channels”
- Let Karl and friends in or out, keep Nate out
- Annie’s friends (\(A^-\)) and Karl’s (\(K^+\)) mostly inside
- Nate and friends (\(Na^+\)) mostly outside
- Claudia (\(Cl^-\)) tagging along
Ion channels
- Openings in neural membrane
- Selective for specific ions
- Vary in permeability (how readily ions flow)
- Some ions can flow more easily than others at different times
- Types
- Passive/leak (always open)
- Voltage-gated
- Ligand-gated (chemically-gated)
- Transporters/pumps
Figure 7.20: http://www.zoology.ubc.ca/~gardner/F21-08.GIF
Neuron at rest permeable to \(K^+\)
- Permeable: Permits flow across/through
- Passive \(K^+\) channels open
- [\(K^+\)] concentration inside >> outside
- \(K^+\) flows out
- Neuron constantly brings \(K^+\) in
Force of diffusion
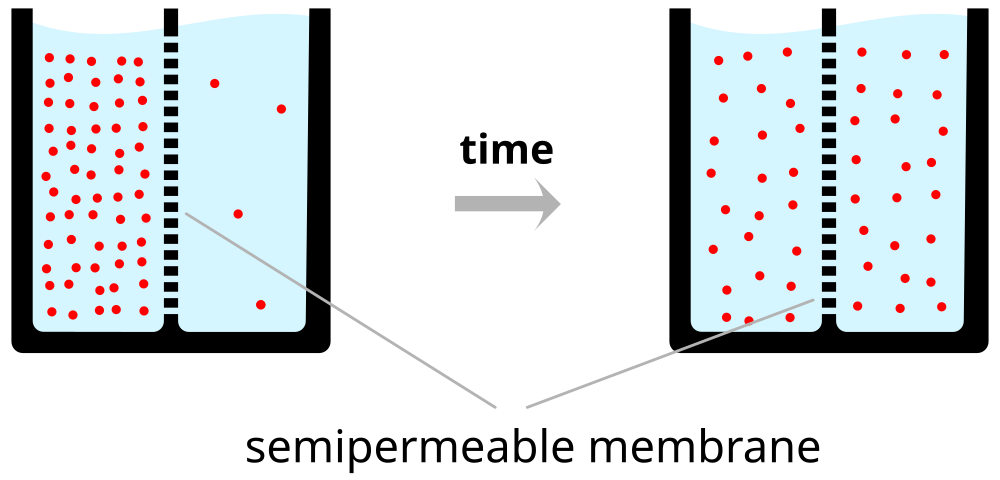
Figure 7.21: https://upload.wikimedia.org/wikipedia/commons/thumb/7/72/Diffusion.en.svg/1000px-Diffusion.en.svg.png
A practical illustration of the force of diffusion.
- Organic anions (\(A^-\)) too large to move outside of cell
- \(A^-\) and \(K^+\) largely in balance == no net internal charge
- \(K^+\) outflow creates charge separation: \(K^+\) (outside) <-> \(A^-\) (inside)
- Charge separation creates a voltage
- Outside +/inside -
- Voltage build-up stops outflow of \(K^+\)
The resting potential
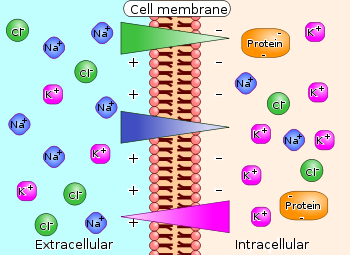
Figure 7.23: The resting potential
Balance of forces in the neuron at rest
- Force of diffusion
- \(K^+\) moves from high concentration (inside) to low (outside)
- Electrostatic force
- Voltage build-up stops \(K^+\) outflow
- Specific voltage that stops flow == equilibrium potential for \(K^+\)+
- \(K^+\) positive, so equilibrium potential negative (w/ respect to outside)
- Equilibrium potential close to neuron’s resting potential
In PSYCH 260, we do not emphasize the calculation of equilibrium potentials and the Nernst equation or the Goldman-Hodgkin-Katz equation.
We provide information about this, and the equivalent circuit model, for your reference.
Equilibrium potential and Nernst equation
Equilibrium potentials calculated under typical conditions
| Ion | [inside] | [outside] | Voltage |
|---|---|---|---|
| \(K^+\) | ~150 mM | ~4 mM | ~ -90 mV |
| \(Na^+\) | ~10 mM | ~140 mM | ~ +55-60 mV |
| \(Cl^-\) | ~10 mM | ~110 mM | - 65-80 mV |
Neuron resting potential ≠ \(K^+\) equilibrium potential
- Resting potential not just due to \(K^+\)
- Other ions flow
- Resting potential == net effects of all ion flows across membrane
- Goldman-Hodgkin-Katz equation
\(Na^+\) role
- \(Na^+\) concentrated outside neuron
- Membrane at rest not very permeable to \(Na^+\)
- Some, but not much \(Na^+\) flows in
- \(Na^+\) has equilibrium potential ~ + 60 mV
- Equilibrium potential is positive (with respect to outside)
- Would need positive interior to keep \(Na^+\) from flowing in
Action potential
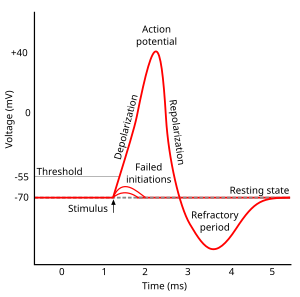
Figure 7.27: The action potential: https://upload.wikimedia.org/wikipedia/commons/thumb/4/4a/Action_potential.svg/300px-Action_potential.svg.png
Phases of the action potential
- Threshold of excitation
- Increase (rising phase/depolarization)
- Peak
- at positive voltage
- Decline (falling phase/repolarization)
- Return to resting potential (refractory period)
| Phase | Neuron State |
|---|---|
| Rise to threshold | + input makes membrane potential more + |
| Rising phase | Voltage-gated \(Na^+\) channels open, \(Na^+\) flows in |
| Peak | Voltage-gated \(Na^+\) channels close and deactivate; voltage-gated \(K^+\) channels open |
| Falling phase | \(K^+\) flows out |
| Refractory period | \(Na^+\)/\(K^+\) pump restores [\(Na^+\)], [\(K^+\)]; voltage-gated \(K^+\) channels close |
What’s a \(Na^+\)/\(K^+\) pump?
- Enzyme – \(Na^+\)/\(K^+\) ATP-ase – embedded in neuron membrane
- Pumps \(Na^+\) and \(K^+\) against concentration gradients
- \(Na^+\) out; \(K^+\) in
- Uses adensosine triphosphate (ATP) form of chemical energy
Figure 7.28: Sodium/Potassium pump: https://commons.wikimedia.org/wiki/File:Scheme_sodium-potassium_pump-en.svg
Refractory phases (periods)
Generating action potentials
- Axon hillock
- Portion of soma adjacent to axon
- Integrates/sums input to soma
- Axon initial segment
- Umyelinated portion of axon adjacent to soma
- Voltage-gated \(Na^+\) and \(K^+\) channels exposed
- If sum of input to soma > threshold, voltage-gated \(Na^+\) channels open
Axon Hillock” by M.aljar3i - Own work. Licensed under CC BY-SA 3.0 via Commons
How action potentials propagate
- Propagation
- move down axon, away from soma, toward axon terminals.
Axon is like an electrical cable
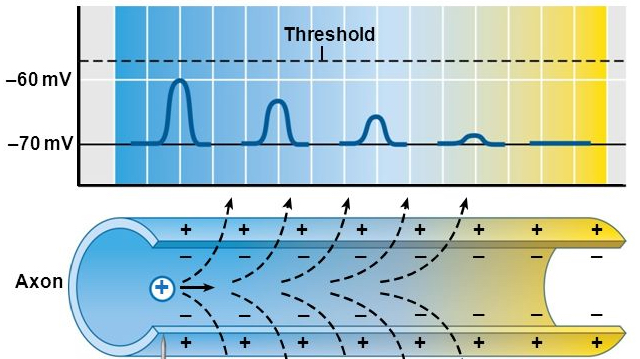
Figure 7.29: http://pittmedneuro.com/synaptic.html
Propagation in unmyelinated axon
- Each segment “excites” the next
Figure 7.30: World record for the wave: https://www.youtube.com/watch?v=H0K2dvB-7WY
Propagation in myelinated axon
- AP “jumps” between Nodes of Ranvier via saltatory conduction
- Nodes of Ranvier == unmyelinated sections of axon
- voltage-gated \(Na^+\), \(K^+\) channels exposed
- current flows through/down myelinated segments
Conduction velocities
- Axons carry information at different rates
- More myelin -> faster
- Larger diameter axon -> faster
- PNS seems to prioritize
- Somatosensory information & muscle control
Information processing
- AP amplitudes don’t vary (much)
- All or none
- \(Na^+\)/\(K^+\) pumps working all the time
- \([K^+]\) & \([Na^+]\) don’t vary much, so
- \(V_{K^+}\) & \(V_{Na^+}\) don’t vary much
- AP frequency and timing vary
- Rate vs. timing codes
- Neurons use both
Figure 7.31: Hodgkin-Huxley: https://www.youtube.com/watch?v=k48jXzFGMc8
The Hodgkin-Huxley (HH) model
By Krishnavedala - Own work, CC0, Link
HH model: Membrane as simple circuit
- Membrane as capacitor (C): stores charge
- Ion channels: resistors that can vary in conductance (\(g=\frac{1}{R}\))
- Ion flows create current (I)
- Ohms Law: \(V=\frac{I}{g}\) or \(Vg=I\)