Making and visualizing data

Published

February 20, 2025

Modified

February 11, 2025

About

This tutorial shows how we can construct data of different types.

The material serves as a companion to the classes on making data, figure types, and figure components.

Code 
# Load required package dependencies "quietly"
suppressPackageStartupMessages(library(ggplot2))
suppressPackageStartupMessages(library(ggmosaic))
suppressPackageStartupMessages(library(dplyr))
suppressPackageStartupMessages(library(ggpattern))
suppressPackageStartupMessages(library(fillpattern))

Nominal data

Let’s focus on nominal or categorical data, specifically the favorite colors of some imaginary set of people.

Code 
# Make an array of color names
colors <- c("red", "orange", "yellow", "green", "cyan", "blue", "violet", "white", "black", "gray")

There are n=10 colors in this set.

Your turn

Why are these data nominal or nominally scaled? Or rather, why aren’t they ordinal, interval, or ratio?

Generating

For demonstration purposes, we want to take some number of random samples of these colors. Let’s pick n=200 and sample with replacement (replace=TRUE in the code below), meaning that we could have any number of colors in our sample of 200 imaginary people.

Code 
# Use `sample()` to pick a random sample of these *with* replacement so that 
# the numbers/color differ.
our_color_sample <- sample(colors, size=200, replace=TRUE)
our_color_sample
  [1] "green"  "black"  "cyan"   "black"  "violet" "cyan"   "cyan"   "green" 
  [9] "green"  "violet" "black"  "violet" "white"  "cyan"   "black"  "cyan"  
 [17] "violet" "orange" "red"    "violet" "blue"   "violet" "orange" "cyan"  
 [25] "gray"   "white"  "green"  "green"  "orange" "orange" "green"  "gray"  
 [33] "white"  "orange" "violet" "blue"   "white"  "blue"   "black"  "gray"  
 [41] "red"    "red"    "violet" "black"  "cyan"   "green"  "blue"   "white" 
 [49] "gray"   "green"  "white"  "blue"   "yellow" "white"  "yellow" "cyan"  
 [57] "white"  "cyan"   "cyan"   "violet" "red"    "yellow" "yellow" "red"   
 [65] "red"    "green"  "red"    "violet" "red"    "green"  "black"  "yellow"
 [73] "yellow" "white"  "green"  "white"  "yellow" "violet" "orange" "gray"  
 [81] "black"  "black"  "violet" "white"  "yellow" "orange" "green"  "blue"  
 [89] "violet" "orange" "yellow" "black"  "gray"   "blue"   "cyan"   "orange"
 [97] "cyan"   "violet" "violet" "black"  "cyan"   "white"  "orange" "red"   
[105] "violet" "black"  "green"  "orange" "yellow" "cyan"   "blue"   "cyan"  
[113] "cyan"   "green"  "gray"   "white"  "green"  "green"  "violet" "cyan"  
[121] "violet" "yellow" "cyan"   "blue"   "blue"   "orange" "yellow" "orange"
[129] "red"    "violet" "orange" "gray"   "yellow" "yellow" "cyan"   "blue"  
[137] "orange" "violet" "violet" "red"    "black"  "violet" "yellow" "green" 
[145] "blue"   "blue"   "green"  "cyan"   "black"  "yellow" "cyan"   "green" 
[153] "orange" "black"  "blue"   "green"  "blue"   "cyan"   "white"  "gray"  
[161] "green"  "cyan"   "white"  "blue"   "blue"   "blue"   "white"  "cyan"  
[169] "yellow" "orange" "green"  "gray"   "black"  "gray"   "cyan"   "orange"
[177] "white"  "red"    "orange" "green"  "white"  "blue"   "orange" "red"   
[185] "gray"   "violet" "gray"   "gray"   "gray"   "blue"   "green"  "blue"  
[193] "orange" "cyan"   "red"    "blue"   "yellow" "blue"   "orange" "yellow"

On its own, that’s not especially easy to visualize. What if we sorted it?

Code 
sort(our_color_sample)
  [1] "black"  "black"  "black"  "black"  "black"  "black"  "black"  "black" 
  [9] "black"  "black"  "black"  "black"  "black"  "black"  "black"  "black" 
 [17] "blue"   "blue"   "blue"   "blue"   "blue"   "blue"   "blue"   "blue"  
 [25] "blue"   "blue"   "blue"   "blue"   "blue"   "blue"   "blue"   "blue"  
 [33] "blue"   "blue"   "blue"   "blue"   "blue"   "blue"   "blue"   "cyan"  
 [41] "cyan"   "cyan"   "cyan"   "cyan"   "cyan"   "cyan"   "cyan"   "cyan"  
 [49] "cyan"   "cyan"   "cyan"   "cyan"   "cyan"   "cyan"   "cyan"   "cyan"  
 [57] "cyan"   "cyan"   "cyan"   "cyan"   "cyan"   "cyan"   "cyan"   "cyan"  
 [65] "cyan"   "gray"   "gray"   "gray"   "gray"   "gray"   "gray"   "gray"  
 [73] "gray"   "gray"   "gray"   "gray"   "gray"   "gray"   "gray"   "gray"  
 [81] "green"  "green"  "green"  "green"  "green"  "green"  "green"  "green" 
 [89] "green"  "green"  "green"  "green"  "green"  "green"  "green"  "green" 
 [97] "green"  "green"  "green"  "green"  "green"  "green"  "green"  "green" 
[105] "orange" "orange" "orange" "orange" "orange" "orange" "orange" "orange"
[113] "orange" "orange" "orange" "orange" "orange" "orange" "orange" "orange"
[121] "orange" "orange" "orange" "orange" "orange" "orange" "red"    "red"   
[129] "red"    "red"    "red"    "red"    "red"    "red"    "red"    "red"   
[137] "red"    "red"    "red"    "red"    "violet" "violet" "violet" "violet"
[145] "violet" "violet" "violet" "violet" "violet" "violet" "violet" "violet"
[153] "violet" "violet" "violet" "violet" "violet" "violet" "violet" "violet"
[161] "violet" "violet" "violet" "white"  "white"  "white"  "white"  "white" 
[169] "white"  "white"  "white"  "white"  "white"  "white"  "white"  "white" 
[177] "white"  "white"  "white"  "white"  "white"  "yellow" "yellow" "yellow"
[185] "yellow" "yellow" "yellow" "yellow" "yellow" "yellow" "yellow" "yellow"
[193] "yellow" "yellow" "yellow" "yellow" "yellow" "yellow" "yellow" "yellow"

Still not all that helpful.

Summarizing

What can we say to summarize categorical data?

We can report the number of total responses.

Code 
length(our_color_sample)
[1] 200

We can report the number of unique categories.

Code 
length(unique(our_color_sample))
[1] 10

We can report the number of responses per category.

Code 
colors_df <- data.frame(favorite_color = our_color_sample)

xtabs(formula = ~favorite_color, data = colors_df)
favorite_color
 black   blue   cyan   gray  green orange    red violet  white yellow 
    16     23     26     15     24     22     14     23     18     19

Visualizing

Single nominal variables don’t offer us many options for visualization. A bar plot showing the number of observations in each category seems to be it.

Code 
colors_df |>
  ggplot() +
  aes(x = favorite_color) +
  geom_bar(stat = "count")
Figure 1: A black and white barplot of the random favorite color data

We can also add colors to the bars.

Code 
colors_df |>
  ggplot() +
  aes(x = favorite_color, fill = favorite_color) +
  geom_bar() +
  scale_discrete_manual(aesthetics = c("color", "fill"),
                        values = sort(colors))
Figure 2: A colorful barplot of the random favorite color data

We can think of this as mapping the name of the color category in our data to the way that category is represented in our figure.

We can flip the axis just for fun. Which is more readable?

Horizontal barplot

Code 
colors_df |>
  ggplot() +
  aes(x = favorite_color, fill = favorite_color) +
  scale_fill_identity() +
  geom_bar() +
  coord_flip()
Figure 3: A colorful horizontal barplot of the random favorite color data

Bar/column with textures

Sometimes we don’t want to use color to distinguish nominal categories.

Code 
colors_df |>
  ggplot() +
  aes(x = favorite_color, fill = favorite_color) +
  geom_bar(aes(y = after_stat(count))) +
  scale_fill_pattern() + # from package 'fillpattern' 
  theme(legend.position = "none")
Figure 4: A barplot of the random favorite color data using textures

Or, we want to use some different textures and have control over them.

Code 
colors_xtab <- data.frame(table(colors_df))
names(colors_xtab) <- c("favorite_color", "count")

colors_xtab |>
  ggplot() +
  aes(x = favorite_color, y = count) +
  # From package 'ggpattern'
  # See https://r-graph-gallery.com/368-black-and-white-barchart.html
  geom_col_pattern(
    aes(
      pattern = favorite_color,
      pattern_angle = favorite_color,
      pattern_spacing = favorite_color
    ),
    fill = 'white',
    color = 'black',
    pattern_density = 0.5,
    pattern_fill = 'black',
    pattern_color = 'darkgrey'
  )
Figure 5: A barplot of the random favorite color data using textures

Ordered

It can be useful to sort the counts of nominal variables to faciliate comparisons among categories.

Code 
colors_df |>
  count(favorite_color) |>
  arrange(desc(n)) |>
  mutate(favorite_color = factor(favorite_color, levels = favorite_color)) |>
  ggplot() +
  aes(x = favorite_color) +
  geom_bar(aes(y = n), stat = "identity")
Figure 6: A horizontal barplot of the random favorite color data, sorted

Let’s order the other ones while we’re at it.

Code 
colors_df |>
  count(favorite_color) |>
  arrange(desc(n)) |>
  mutate(favorite_color = factor(favorite_color, levels = favorite_color)) |>
  ggplot() +
  aes(x = favorite_color, y = n, fill = favorite_color) +
  geom_bar(stat = "identity") +
  scale_fill_pattern() + # from package 'fillpattern'
  theme(legend.position = "none")
Figure 7: A barplot of the random favorite color data using textures
Code 
colors_df |>
  count(favorite_color) |>
  arrange(desc(n)) |>
  mutate(favorite_color = factor(favorite_color, levels = favorite_color)) |>
  ggplot() +
  aes(x = favorite_color, y = n) +
  # From package 'ggpattern'
  # See https://r-graph-gallery.com/368-black-and-white-barchart.html
  geom_col_pattern(
    aes(
      pattern = favorite_color,
      pattern_angle = favorite_color,
      pattern_spacing = favorite_color
    ),
    fill = 'white',
    color = 'black',
    pattern_density = 0.5,
    pattern_fill = 'black',
    pattern_color = 'darkgrey'
  ) +
  theme(legend.position = "none")
Figure 8: A barplot of the random favorite color data using textures

Lollipop chart

The lollipop chart uses less ink, so the ink/data ratio (Tufte, 2001) is higher than with barplots.

Code 
colors_df |>
  count(favorite_color) |>
  arrange(desc(n)) |>
  mutate(favorite_color = factor(favorite_color, levels = favorite_color)) |>
  ggplot() +
    geom_point(aes(
    x = favorite_color,
    y = n,
    color = favorite_color,
    fill = favorite_color
  )) +
  geom_segment(aes(
    x = favorite_color,
    xend = favorite_color,
    y = 0,
    yend = n,
    color = favorite_color
  )) +
  scale_color_identity() +
  scale_fill_identity()
Figure 9: A lollipop plot of the random favorite color data

Stacked barplot

We can also stack them.

Code 
colors_df |>
  count(favorite_color) |>
  ggplot() +
  aes(x = "", y = n, fill = favorite_color) +
  geom_col(position = "stack") +
  scale_fill_identity() +
  xlab("")
Figure 10: A stacked barplot of the random favorite color data

This makes more sense with another nominal variable in the mix.

Let’s add a ‘school’ variable.

Code 
school <- sample(c("psu", "osu", "mich", "usc"), size=200, replace=TRUE)
colors_school_df <- colors_df
colors_school_df$school <- school

Then create the plot.

Code 
colors_school_xtab <- data.frame(table(colors_school_df))
names(colors_school_xtab) <- c("favorite_color", "school", "count")

# colors_school_xtab |>
#   ggplot() +
#   aes(x = school, y=count, fill = favorite_color) +
#   scale_fill_identity() +
#   geom_bar(stat="identity", position="stack")

colors_school_df |> 
  count(school, favorite_color) |> 
  ggplot() + 
  aes(school, n, fill = favorite_color) + 
  scale_fill_identity() + 
  geom_bar(stat="identity", position="stack")
Figure 11: A stacked barplot of the random favorite color data

Stacked barplot alternative

Code 
colors_school_xtab |>
  ggplot() +
  aes(x = favorite_color, y=count, fill = school) +
  geom_bar(stat="identity", position="stack")
Figure 12: Another stacked barplot of the random favorite color data.

Dodged barplot

Using the ‘dodge’ parameter is another way to show data with two categorical variables.

Code 
colors_school_xtab |>
  ggplot() +
  aes(x = school, y=count, fill = favorite_color) +
  scale_fill_identity() +
  geom_bar(stat="identity", position="dodge")
Figure 13: A horizontal barplot of the random favorite color data

Pie chart

Code 
colors_xtab <- data.frame(table(colors_df))
names(colors_xtab) <- c("favorite_color", "count")

colors_xtab |>
  ggplot(aes(x = "", y = count, fill = favorite_color)) +
  geom_bar(stat = "identity", width = 1) +
  coord_polar("y", start = 0) +
  scale_fill_identity()
Figure 14: A piechart of the random favorite color data

Ring chart

Code 
# https://r-graph-gallery.com/128-ring-or-donut-plot.html

# Compute percentages
colors_xtab$fraction = colors_xtab$count / sum(colors_xtab$count)

# Compute the cumulative percentages (top of each rectangle)
colors_xtab$ymax = cumsum(colors_xtab$fraction)

# Compute the bottom of each rectangle
colors_xtab$ymin = c(0, head(colors_xtab$ymax, n = -1))

# Make the plot
colors_xtab |>
  ggplot(aes(
    ymax = ymax,
    ymin = ymin,
    xmax = 4,
    xmin = 3,
    fill = favorite_color
  )) +
  geom_rect() +
  coord_polar(theta = "y") + # Try to remove that to understand how the chart is built initially
  xlim(c(2, 4)) + # Try to remove that to see how to make a pie chart
  scale_fill_identity()
Figure 15: A ring/donut chart of the random favorite color data

Mosaic plot

Code 
ggplot(data = colors_school_df) +
  geom_mosaic(aes(x = product(favorite_color, school), fill = favorite_color)) +   
  labs(y="Favorite", x="School", title = "Favorite colors by school") +
  scale_fill_identity()
Warning: The `scale_name` argument of `continuous_scale()` is deprecated as of ggplot2
3.5.0.
Warning: The `trans` argument of `continuous_scale()` is deprecated as of ggplot2 3.5.0.
ℹ Please use the `transform` argument instead.
Warning: `unite_()` was deprecated in tidyr 1.2.0.
ℹ Please use `unite()` instead.
ℹ The deprecated feature was likely used in the ggmosaic package.
  Please report the issue at <https://github.com/haleyjeppson/ggmosaic>.
Figure 16: A mosaic chart of the random favorite color by school data

Ordinal data

We usually consider colors as nominal or categorical variables. But the physical input to the visual system is continuous.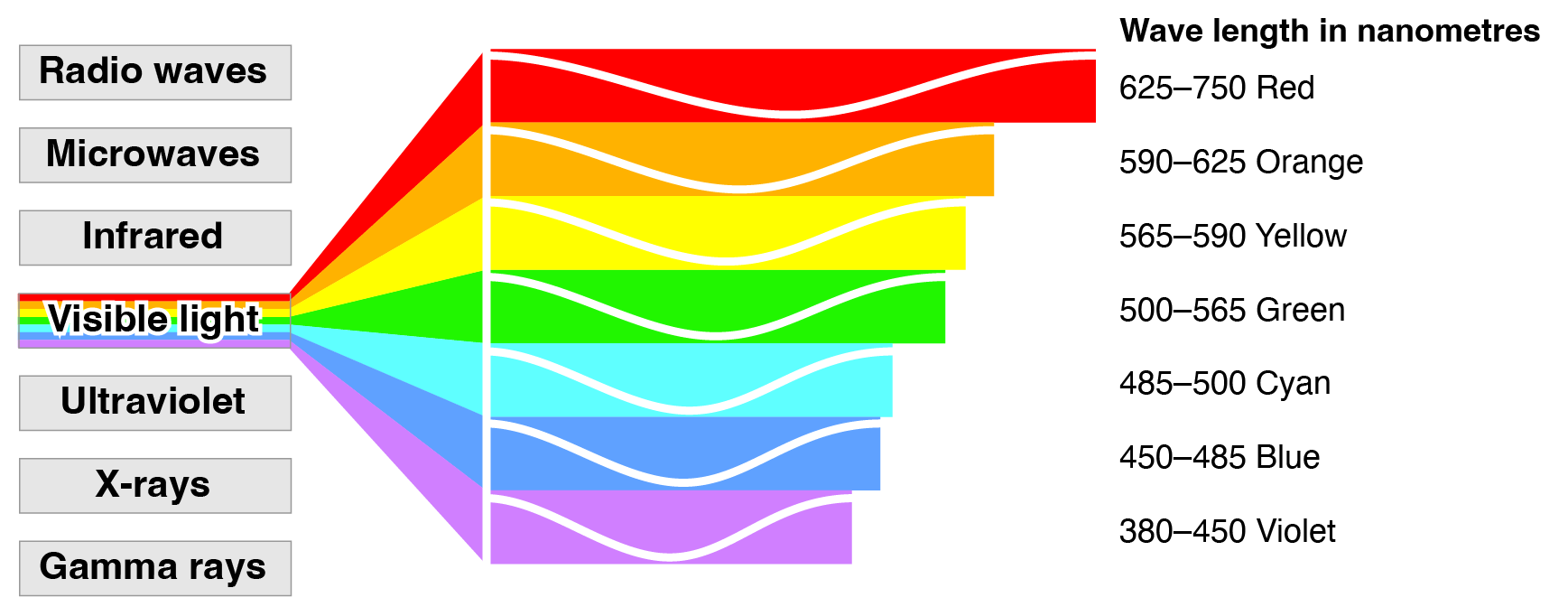

https://rmit.pressbooks.pub/colourtheory1/part/2-colour-theory-the-visible-spectrum/

https://rmit.pressbooks.pub/colourtheory1/part/2-colour-theory-the-visible-spectrum/

The continuous variable that underlies color is wavelength, a property of electromagnetic radiation. The human visual system maps patterns of physical wavelength to the psychological dimension of color.

Curiously, human color perception shows that this psychological mapping wraps in a circular way that physical wavelength does not.

https://pixabay.com/vectors/rainbow-colors-circle-color-spectrum-154569/

https://pixabay.com/vectors/rainbow-colors-circle-color-spectrum-154569/

Generating

But rather than dive down that particular rat hole now, let’s make some ordinal data from the random color dataset. Imagine that we had n=50 participants and each gave a rating to these colors. The ratings had numbers, with 1 assigned to the participant’s first choice, and 4 assigned to the fourth choice. We won’t keep track of the specific users at this point.

Code 
ratings <- c("1st", "2nd", "3rd", "4th")

our_rating_sample <- sample(ratings, size=200, replace=TRUE)
colors_rating_df <- colors_df
colors_rating_df$rating <- our_rating_sample

colors_rating_xtab <- data.frame(table(colors_rating_df))
names(colors_rating_xtab) <- c("favorite_color", "rating", "count")

Visualizing

Many of the same plot types are available for ordinal data.

Bar plot ordinal dodge

Code 
colors_rating_xtab |>
  ggplot() +
  aes(x=rating, y=count, fill = favorite_color) +
  # aes(x = favorite_color, y = school, fill = favorite_color) +
  scale_fill_identity() +
  geom_bar(stat="identity", position="dodge")
Figure 17: A barplot of the random favorite color data with an ordinal rating

Bar plot ordinal stacked

Code 
# colors_rating_xtab |>
#   ggplot() +
#   aes(x=favorite_color, y=count, fill = favorite_color) +
#   scale_fill_identity() +
#   geom_bar(stat="identity", position="dodge")

colors_rating_xtab |>
  ggplot() +
  aes(x = rating, y=count, fill = favorite_color) +
  scale_fill_identity() +
  geom_bar(stat="identity", position="stack")
Figure 18: A stacked barplot of the random favorite color data with an ordinal rating

Bar plot ordinal stacked alternative

Code 
colors_rating_xtab |>
  ggplot() +
  aes(x = favorite_color, y=count, fill = rating) +
  geom_bar(stat="identity", position="stack")
Figure 19: Another stacked barplot of the random favorite color data with an ordinal rating

Continuous data

Generating

Let’s imagine that we are studying a group of people who vary in age and body temperature.

We’ll assume that they are healthy–fever free.

And we assume that we’re sampling uniformly across children (0-18 years) and adults (18-85).

Code 
n_kids <- 100
n_adults <- 100
age_days_kids <- runif(n_kids, 0, 18*365)
age_days_adults <- runif(n_adults, 18*365+1, 85*365)

# https://www.webmd.com/first-aid/normal-body-temperature
body_temps_kids <- runif(n_kids, 95.9, 99.5)
body_temps_adults <- runif(n_adults, 97, 99)

age_days <- c(age_days_kids, age_days_adults)
body_temp_F <- c(body_temps_kids, body_temps_adults)

age_temp_df <- data.frame(age_days = age_days, body_temp = body_temp_F)

# Mix them up a bit
age_temp_df <- age_temp_df[sample(nrow(age_temp_df)),]

Visualizing

To visualize continuous data, we have to decide what question(s) we want to answer.

Scatterplot

The simplest visualization of two continuous variables is a scatterplot.

Code 
age_temp_df |>
  ggplot() +
  aes(x = age_days, y = body_temp) +
  geom_point()
Figure 20: A scatterplot of the age and body temperature data.

Histograms

Code 
age_temp_df |>
  ggplot() +
  aes(x = age_days) +
  geom_histogram()
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Figure 21: A histogram of the age data.
Code 
age_temp_df |>
  ggplot() +
  aes(x = body_temp) +
  geom_histogram()
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Figure 22: A histogram of the body temperature data.

Violin plots

Code 
age_temp_df |>
  ggplot() +
  aes(x = age_days, y = "") +
  geom_violin()
Figure 23: A violin plot of the age data.
Code 
age_temp_df |>
  ggplot() +
  aes(y = "", x = body_temp) +
  geom_violin()
Figure 24: A violin plot of the body temperature data.

Density

Code 
age_temp_df |>
  ggplot() +
  aes(x = age_days) +
  geom_density()
Figure 25: A density plot of the age data.
Code 
age_temp_df |>
  ggplot() +
  aes(x = body_temp) +
  geom_density()
Figure 26: A density plot of the body temperature data.

Boxplot

Code 
age_temp_df |>
  ggplot() +
  aes(x = age_days) +
  geom_boxplot()
Figure 27: A boxplot of the age data.
Code 
age_temp_df |>
  ggplot() +
  aes(x = body_temp) +
  geom_boxplot()
Figure 28: A boxplot of the body temperature data.

Violin + Boxplot

Code 
age_temp_df |>
  ggplot() +
  aes(x = age_days, y = "") +
  geom_violin() +
  geom_boxplot(alpha = .4)
Figure 29: A combined violin/boxplot of the age data.
Code 
age_temp_df |>
  ggplot() +
  aes(x = body_temp, y = "") +
  geom_violin() +
  geom_boxplot(alpha = .4)
Figure 30: A combined violin/boxplot of the body temperature data.

Violin + Boxplot + Scatter

Code 
age_temp_df |>
  ggplot() +
  aes(x = age_days, y = "") +
  geom_violin() +
  geom_boxplot(alpha = .4) +
  geom_jitter(width = 0, height = .2)
Figure 31: A combined violin/boxplot/scatterplot of the age data.
Code 
age_temp_df |>
  ggplot() +
  aes(x = body_temp, y = "") +
  geom_violin() +
  geom_boxplot(alpha = .4) +
  geom_jitter(width = 0, height = .2)
Figure 32: A combined violin/boxplot/scatterplot of the body temperature data.

References

Tufte, E. R. (2001). The Visual Display of Quantitative Information. Graphics Pr.