Cellular neuroscience

PSY 511.003

Published

January 31, 2024

Why animals need nervous systems

Sterling & Laughlin, 2015

Escherichia Coli (E. Coli)
- Tiny, single-celled bacterium
- Feeds on glucose
- Chemo (“taste”) receptors on surface membrane
- Flagellum for movement
- Food concentration regulates duration of “move” phase
- ~4 ms for chemical signal to diffuse from anterior/posterior

Paramecium
- 300K larger than E. Coli
- Propulsion through coordinated beating of cilia
- Diffusion from head to tail ~40 s!
- Use electrical signaling instead
  - $Na^+$ channel opens (e.g., when stretched)
  - Voltage-gated $Ca^{++}$ channels open, $Ca^{++}$ enters, triggers cilia
  - Signal across cell within ms

C Elegans swimming.

Caenorhabditis Elegans (C. Elegans)
- ~10x larger than paramecium
- 302 neurons + 56 glial cells (out of 959)
- Swim, forage, mate

Neural communication types

Electrical
- Fast(er) (10-100x)
- Within neurons
- From one part of body to another
- Point-to-point connections for specificity
- Metabolically costly to create & maintain
- How to reliably send a message from here to there?
Chemical
- Diffusion slow(er)
- Within & between neurons
- or other cells
- Molecular matching (binding) for specificity
- Metabolically efficient

So, why do large/complex animals need nervous systems?

Cellular neuroanatomy

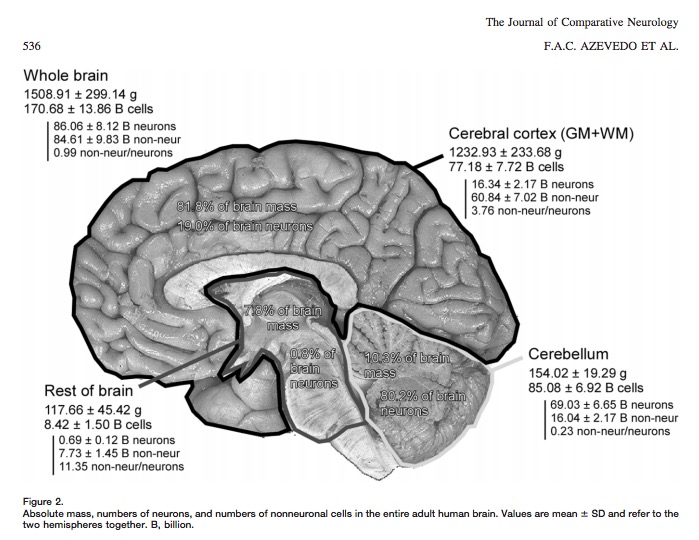
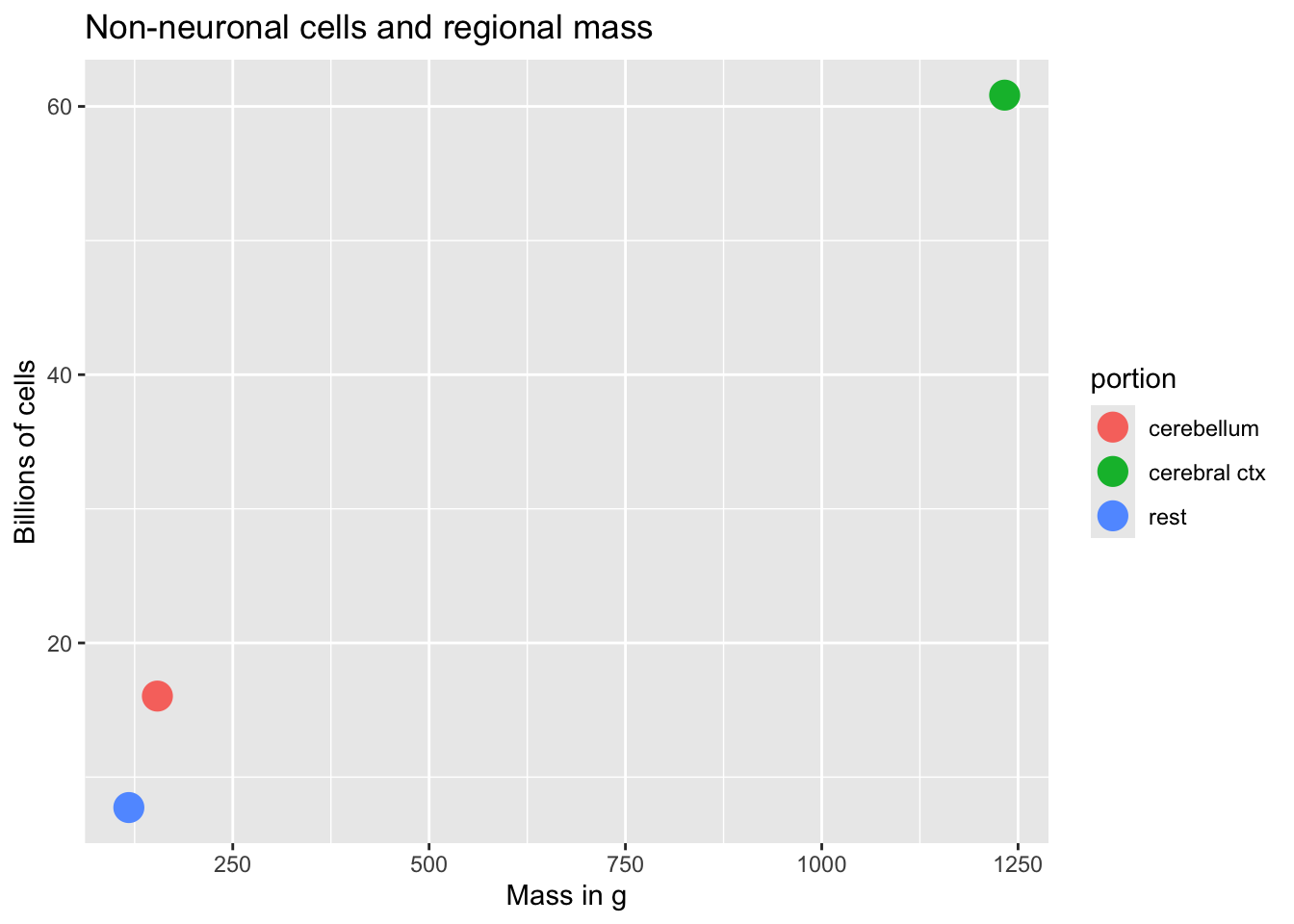
How many neurons and glia?

Old “lore”: ~100 billion neurons
New estimate (Azevedo et al., 2009):
- ~86 +/- 8 billion neurons
- ~85 +/- 9 billion glia

“These findings challenge the common view that humans stand out from other primates in their brain composition and indicate that, with regard to numbers of neuronal and nonneuronal cells, the human brain is an isometrically scaled-up primate brain.”

[@azevedo2009equal]

Glia (neuroglia)

Functions
- Structural support
- Metabolic support
- Brain development

Astrocytes

“Star-shaped”
Probably most numerous cell type in CNS
Physical and metabolic support
- Support blood/brain barrier
- Regulate local blood flow

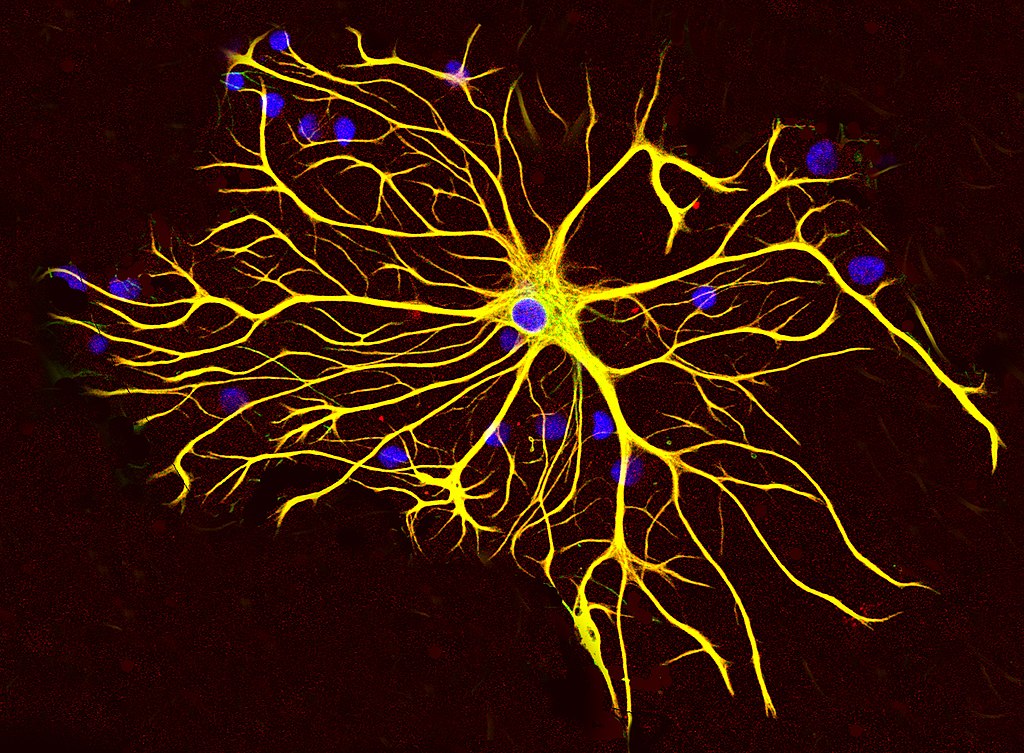
Interact with neurons
- Ion (Ca++/K+) buffering
- Neurotransmitter (e.g., glutamate) buffering

Shape brain development, contribute to synaptic plasticity
Disruption linked to cognitive impairment, disease (Chung, Welsh, Barres, & Stevens, 2015)

Myelinating cells

Oligodendrocytes

In brain and spinal cord (CNS)
1:many neurons

Schwann cells

In PNS
1:1 neuron
Facilitate neuro-regeneration

TV show preference mnemonics: COPS/SPOC

Microglia

Phagocytosis
Clean-up damaged, dead tissue
Role in ‘pruning’ of synapses in normal development

Neurons

What makes neurons “special”

Long-lived (most generated b/w 3-25 weeks gestational age)
Extended branching (dendrites and axons)
Electrically excitable
Connect to small #s of other cells via synapses
Release neurotransmitters

Macrostructure

Dendrites
Soma
Axons
Terminal buttons (boutons)

Dendrites

Majority of input to neuron
Passive (do not generate current flows) vs. active (generate current flows like axons)
“Polarized” or directional information flow

Dendritic Spines

Concentrate effects of local current flows, biochemical reactions

Soma (cell body)

Varied shapes
Nucleus
- Chromosomes
Organelles
- Mitochondria
- Smooth and Rough Endoplasmic reticulum (ER)

Axons

Axon hillock

Transitional zone between soma and axon

Initial segment

Action potential generated

Nodes of Ranvier

Gaps in myelin sheath
Neuronal membrane exposed to extracellular space
Action potential regenerates

Axon terminals

Synaptic bouton (terminal button)

Synapse (~5-10K per neuron)
Pre- (sending side) and postsynaptic (receiving side) membranes
Synaptic cleft
Synaptic vesicles
- Store/release neurotransmitters

Autoreceptors & transporters

(Figure 1 from Torres, Gainetdinov, & Caron, 2003). Monoamine transporters are localized to perisynaptic sites, where they are crucial for the termination of monoamine transmission and the maintenance of presynaptic monoamine storage. Several selective pharmacological agents acting at each monoamine transporter are shown. Amph., amphetamine; DA, dopamine; DAT, Dopamine transporter; L-DOPA, L-3,4-dihydroxyphenylalanine; 5-HT, 5-hydroxytryptamine; MPP+, 1-methyl-4-phenylpyridinium; MDMA, (+)-3,4-methylenedioxymethamphetamine; NA, noradrenaline; NET, noradrenaline transporter; SERT, 5-HT transporter

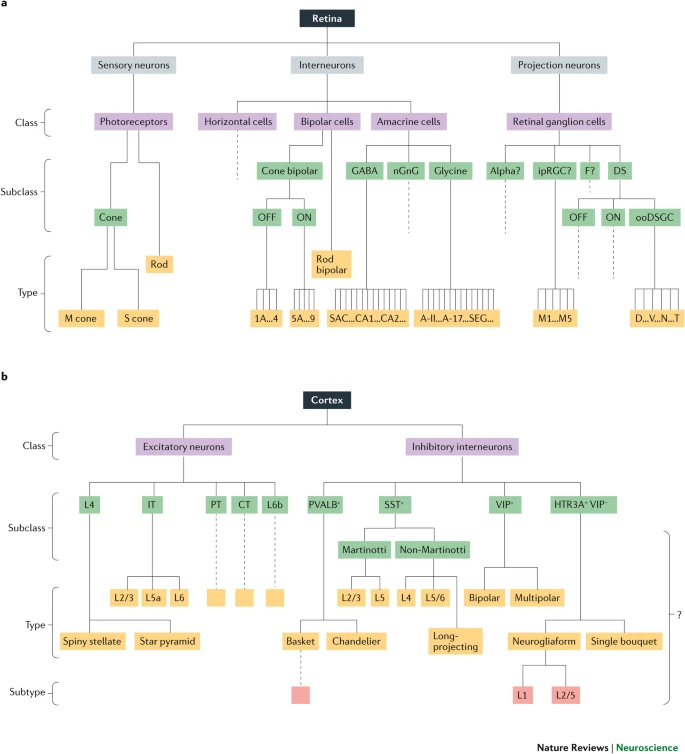
Classifying neurons

Functional role
- Input (sensory), output (motor/secretory), interneurons
Anatomy
- Unipolar
- Bipolar
- Multipolar

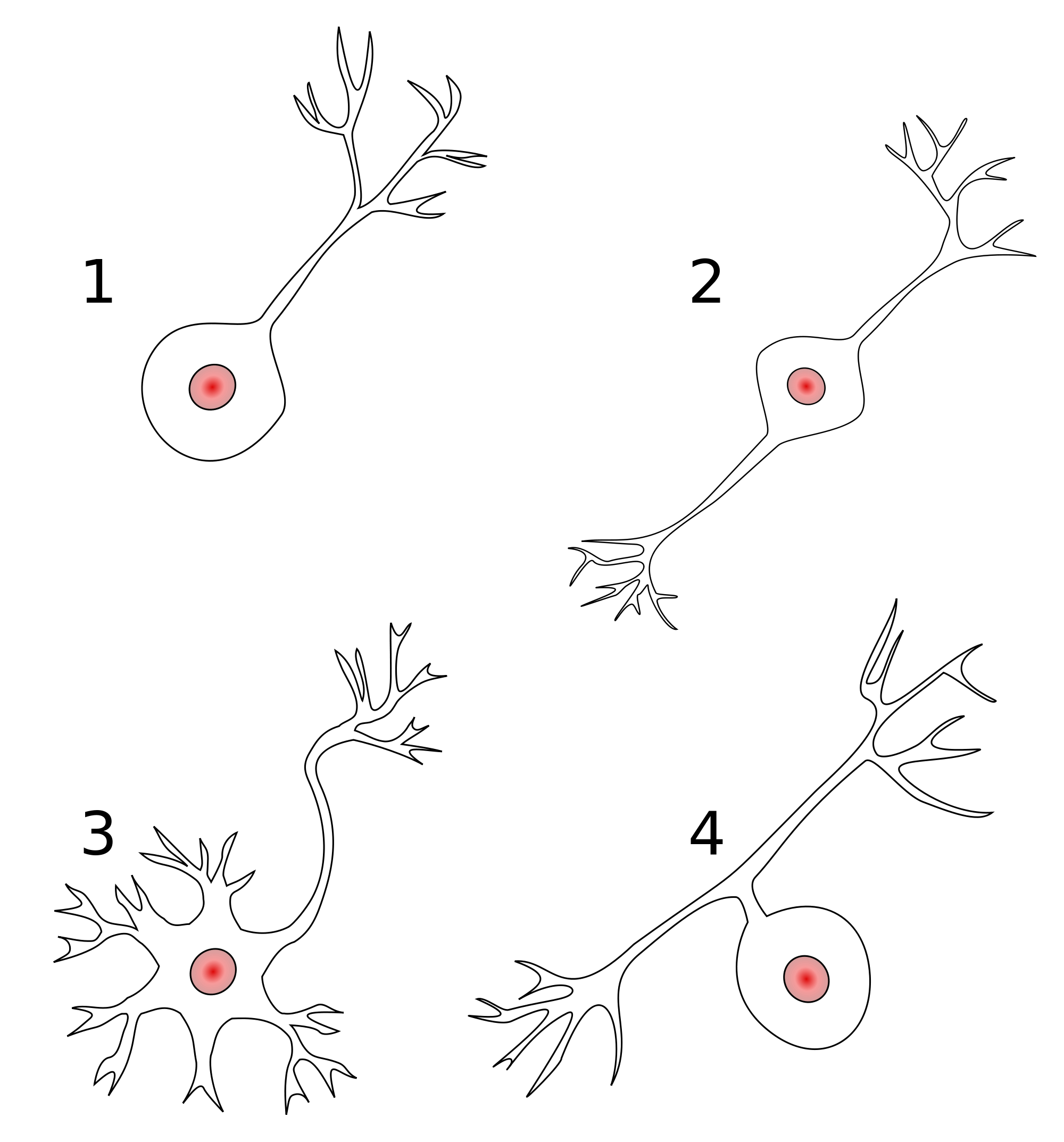
By specific anatomy
- Pyramidal cells
- Stellate cells
- Purkinje cells
- Granule cells

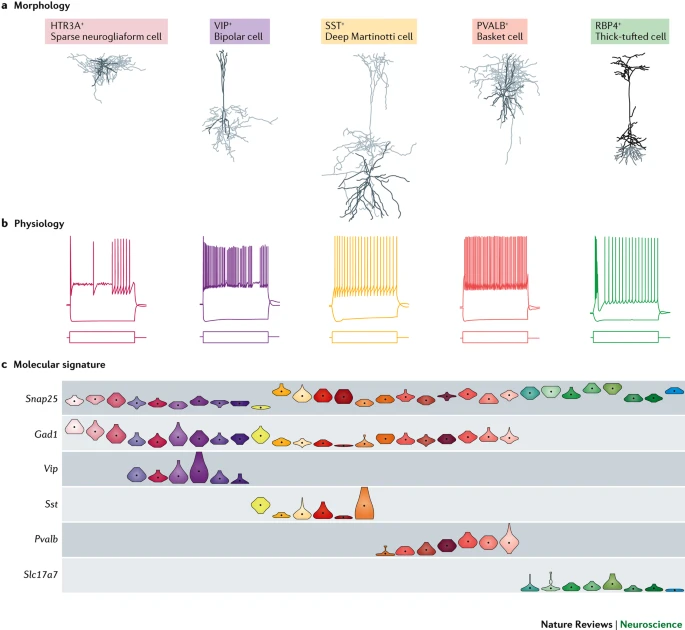
Pyramidal cell (left) | Stellate cell (right) from Wikipedia

Morphology, physiology, gene transcription

(Figure 1 from Zeng & Sanes, 2017). Neurons can be classified using morphological, physiological and molecular criteria. a | Representative examples of five subclasses of cortical neurons obtained from brain slices. The cells were filled with biocytin, stained and imaged following patch clamp recording (see part b). Each subclass has distinct morphological features. For the four interneurons on the left, the dendrites are shown in dark grey and the axons in light grey. The soma of the 5-hydroxytryptamine receptor 3A-expressing (HTR3A+) sparse neuro- gliaform cell is located in layer 1, and its axons are also concentrated in this layer. The vasoactive intestinal peptide-expressing (VIP+) bipolar cell has a characteristic bipolar dendritic extension. The soma of the somatostatin-expressing (SST+) deep Martinotti cell is located in layer 5/6, and its axons extend upward into layer 1. The parvalbumin-expressing (PVALB+) basket cell has basket-like axonal arborisation. For the excitatory neuron on the right, the apical dendrites are shown in dark grey and the basal dendrites in light grey. This is a layer 5, thick-tufted cell from a retinol-binding protein 4 (Rbp4) gene promoter-driven Cre-expressing mouse. The cell features thick apical dendritic tufts extending into layer 1. These morphological features are consistent with those described in published reports49,130,140. b | Differential electrophysiological responses of the five subclasses of neurons shown in part a to square pulses of current in patch clamp recordings. For example, the HTR3A+ cell is late spiking, whereas the PVALB+ cell is fast spiking. These responses are consistent with those described in published reports49,130,140. c | Differential molecular signatures of the five subclasses of cortical neurons illustrated in part a derived from single-cell RNA-sequencing data. The violin plot shows the collective gene expression profile for each gene of all the cells in a type (cluster). We define the smallest discrete clusters of cells as types and the aggregates of types that share common features as classes or subclasses. Each transcriptomic cell type is shown as a column of data points with the same colour (the colour coding corresponds to that of the transcriptomic taxonomy shown in Fig. 5). Shown here are three interneuron cell types expressing Htr3a but notVip, six interneuron cell types expressing Vip, six interneuron cell types expressing Sst and seven interneuron cell types expressing Pvalb. All of the interneurons express glutamate decarboxylase 1 (Gad1). Also shown are eight layer 5 excitatory neuron types, all of which express solute carrier family 17 member 7 (Slc17a7). All of the cells express synaptosome-associated protein 25 (Snap25). The height of each ‘violin’-shaped data point represents the range of expression levels of the gene, and the width represents the proportion of cells displaying a particular level of expression. Parts a and b are from the Allen Cell Types Database (see Further Information). Part c is adapted with permission from Ref. 136.

(Figure 6 from Zeng & Sanes, 2017). The figure shows a proposed hierarchical classification of cells in the retina (a) and cerebral cortex (b). In both areas, individual cell types can be grouped into classes, and intermediate levels of subclasses can be determined based on distinct morphological, physiological and molecular features. Higher-order groupings (such as those shown in part a, including sensory neurons, interneurons and projection neurons) may emerge once enough areas have been provided and compared. Types are the commonly recognized (‘validated’) terminal branches in the current hierarchical arrangement of cell types. Lower-order groupings into subtypes may largely be provisional until additional data are collected that could determine if they could form new types or should be merged into other types. Dashed lines indicate the presence of additional types that cannot be labelled due to lack of space. The question marks in part a indicate that the hierarchical relationship among the indicated cell types remains unclear. The question mark in part b indicates that the status of the cortical cell groups indicated may be either subclasses, types or subtypes. CT, cortico-thalamic neurons; DS, direction-selective retinal ganglion cells (RGCs); F, forkhead box P2 (Foxp2)-expressing RGCs; HTR3A, 5-hydroxytryptamine receptor 3A; ipRGC, intrinsically photosensitive RGCs; IT, intratelencephalic neurons; L4, layer 4; L6b, layer 6b subplate neurons; nGnG, non-GABAergic-non-glycinergic amacrine cells; ooDSGC, ON-OFF direction-selective RGCs; PT, pyramidal tract neurons; PVALB, parvalbumin; SST, somatostatin; VIP, vasoactive intestinal peptide.

(Figure 4 from Boldog et al., 2018). a, Examples of different firing patterns induced by current injections in layer 1 interneurons. Firing pattern of an RC (top), an NGFC (middle), and an unidentified layer 1 interneuron (bottom). b, SVM-based wrapper-feature selection of electrophysiological parameters for the identification of RCs. Anatomically identified RCs (red dots) and other types of interneurons with known morphology (black dots) are mapped to the distribution of electrophysiological features ranked as the two best delineators by SVM. Black lines show the best hyperplane separating RCs from other interneuron types. c,d, RCs exhibit a distinct impedance profile relative to neurogliaform and other human interneurons in layer 1. (c) Individual responses of anatomically identified rosehip (red), neurogliaform (blue), and other (black) interneurons to current injections with an exponential chirp (0.2–200 Hz; top). Traces were normalized to the amplitude of the rosehip response at 200 Hz. (d) Left: normalized impedance (Z) profiles of distinct groups of interneurons. RCs (n=5) had higher impedance in the range of 0.9–12.4 Hz compared to neurogliaform (n=5) and other (n=5) interneurons. Shaded regions represent s.d. Right: impedances were similar at the lowest frequency (Z0.2 Hz; left), but resonance magnitude (Q) calculated as maximal impedance value divided by the impedance at lowest frequency (middle) and frequencies of maximal impedance (fmax; right) showed significant differences (P < 0.05, ANOVA with Bonferroni post hoc correction). e, Automatized selection of recording periods for assessing subthreshold membrane potential oscillations (boxed segments) and detection of bursts (bars) for measuring intraburst spiking frequency demonstrated on an RC response to near-rheobasic stimulation showing stuttering firing behavior. f, Averaged fast fast Fourier transforms (FFTs) of membrane potential oscillations had higher power between 3.8 and 80 Hz in RCs compared to neurogliaform and other interneurons. g, Intraburst frequency of RCs peaked in the gamma range. AP, action potential.

Neurophysiology

Electrical communication

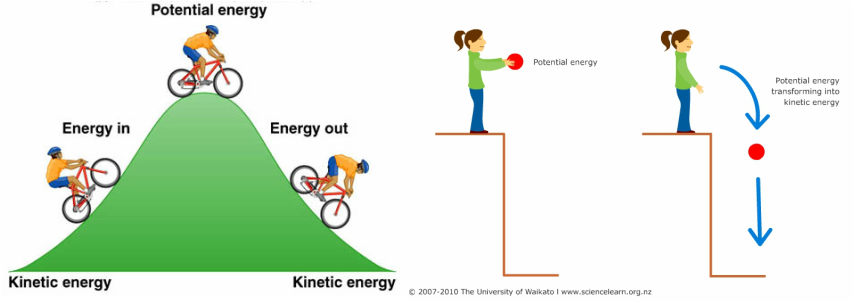
Electrical potential (== voltage)
- Think of potential energy
- Voltage ~ pressure
- Energy that will be released if something changes

Basic principles

\[E = IR\]

Current flow ($I$) across membrane
Membrane varies in resistance ($R$) or permeability ($1/R$) to ion flow
Product $IR$ is electrical voltage $E$

Membrane stores (& releases) charge like capacitor

Resting potential

Potential energy
- Energy that could be released if circumstances change

Measurement
- Electrode on inside
- Electrode on outside (reference)
- Inside - Outside = potential

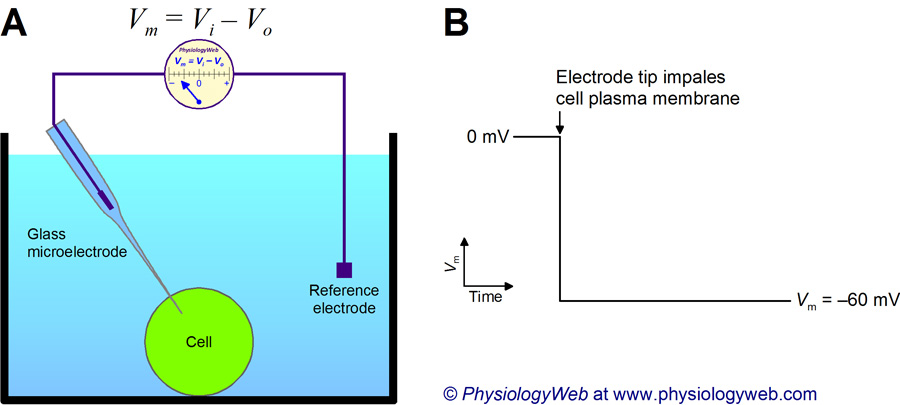
Neuron (and other cells) have potential energy
- Inside is -60-70 mV, with respect to outside
- ~1/20th typical $1.5V$ AAA battery
Like charges repel, opposites attract, so
- Positively charged particles pulled in
- Negatively charged particles pushed out

Contributors to

Ions
- Potassium, $K^+$
- Sodium, $Na^+$
- Chloride, $Cl^-$
- Calcium, $Ca^{++}$
- Organic anions, $A^-$
Ion channels
Separation between charges
A balance of forces

Party metaphor

Annie ($A^-$) was having a party.
- Used to date Nate ($Na^+$), but now sees Karl ($K^+$)
Hired bouncers called
- “The Channels”
- Let Karl and friends in or out, keep Nate out
Annie’s friends ($A^-$) and Karl’s ($K^+$) mostly inside
Nate and friends ($Na^+$) mostly outside
Claude/Claudia ($Cl^-$) tagging along

Ion channels

Macromolecules that form openings in membrane
Different types of subunits

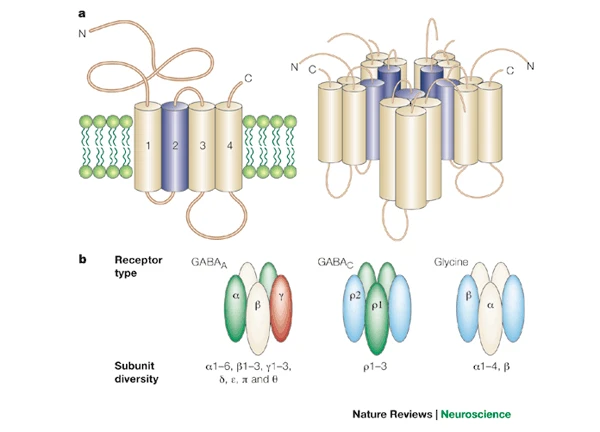
Selective (bind only to some substances, not others)
Vary in permeability (allow some substances to pass more than others)
Types
- Passive/leak
- Voltage-gated
- Ligand-gated (chemically-gated)
- Transporters

Conditions

Neuron at rest permeable to $K^+$

Passive $K^+$ channels open
$[K^+]_{i} >> [K^+]_{o}$
$K^+$ flows out

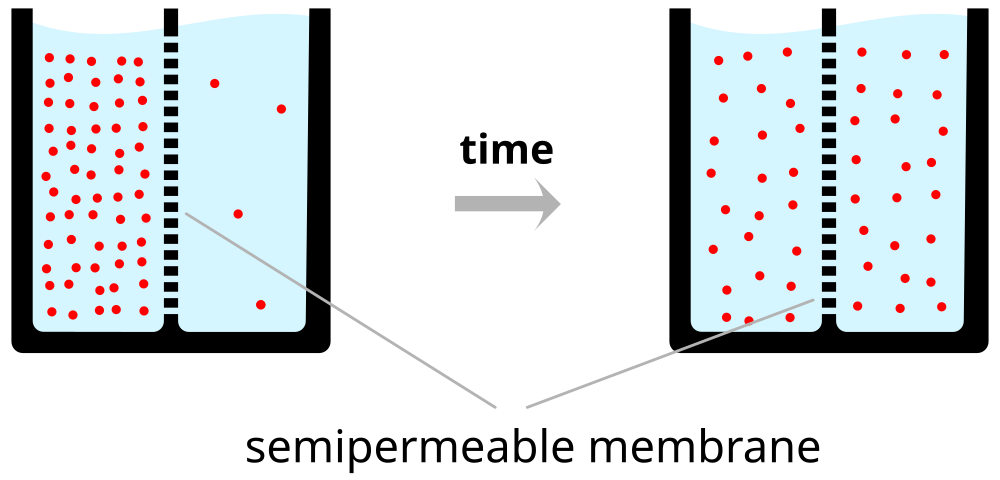
Force of diffusion
- $K^+$ moves from high concentration (~140 mM inside) to low (~4 mM outside)
- $K^+$ outflow would stop when $[K^+]_{o} == [K^2]_{i}$
- But…
Na/Ka-ATPase (Na/K Pump)
- Keeps concentration gradients
- Moves $K+$ in, $Na+$ out
Electrostatic pressure
- $K^+$ has + electric charge
- Movement of charged $K^+$ ions creates current
- Movement of charged $K^+$ ions creates charge separation
  - Some $A^-$ no longer have matching $K^+$
  - Charge separation across membrane creates voltage (~ capacitor)
- Voltage build-up stops $K^+$ outflow
- Voltage magnitude called “reversal potential” or equilibrium potential
- $K^+$ positive, so reversal potential negative (w/ respect to outside)
- $K^+$ reversal potential (~90mV) close to, but more negative than neuron resting potential (-70mV)

Equilibrium potential and the Nernst equation

Neuron at resting potential has low $Na^+$ permeability

$Na^+$ concentrated outside neuron ($[Na^+]_{o}$~145 mM) vs. inside ($[Na^+]_{i}$~12 mM)
Equilibrium potential is positive (with respect to outside)
Some $Na^+$ flows in
Calculate net effects of ion flow across membrane via
Goldman-Hodgkin-Katz equation

Ions contributing to the resting potential

Summary of forces

Ion	Concentration gradient	Force of diffusion	Sign of electrostatic force
$K^+$	$[K^+]_{i} >> [K^+]_{o}$	outward	-
$Na^+$	$[Na^+]_{i} << [Na^+]_{o}$	inward	-

“Driving Force” on a given ion depends on its equilibrium potential AND current membrane potential.
Driving force >> if membrane potential far from equilibrium potential for ion.
Equilibrium potential
- Voltage that keeps current (inside/outside) concentrations the same
- Voltage membrane potential will approach if only that ion flows

Equilibrium potentials

Under typical conditions

Ion	[inside]	[outside]	Voltage
$K^+$	~150 mM	~4 mM	~ -90 mV
$Na^+$	~10 mM	~140 mM	~ +55-60 mV
$Cl-$	~10 mM	~110 mM	- 65-80 mV

Action potential

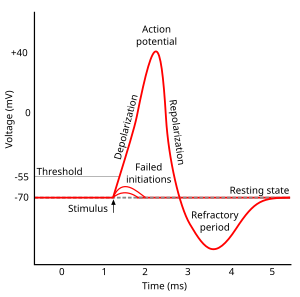
Rapid rise, fall of membrane potential
Threshold of excitation
Increase (rising phase/depolarization)
Peak
- at positive voltage
Decline (falling phase/repolarization)
Return to resting potential (refractory period)

Note

The $K^+$ story

$Na^+$/$K^+$ pump pulls $K^+$ in
$[K^+]_{in}$ (~150 mM) >> $[K^+]_{out}$ (~4 mM)
Outward flow of $K^+$ through passive/leak channels
Outflow stops when membrane potential, $V_m$ = equilibrium potential for $K^+$

Equilibrium potential

Voltage ($V_{K}$) that keeps system in equilibrium
- $[K^+]_{in}$ >> $[K^+]_{out}$
Nernst equation
- $V_{K}$ = $\frac{RT}{(+1)F}ln(\frac{[K^+]_{out}}{[K^+]_{in}})$
- $V_{K}$ = ~ -90 mV
- Negative in/positive out keeps in/out concentration gradient
$K^+$ flows out through passive/leak channels; most remains near membrane
Separation from $A^-$ creates charge $\frac{K+K+K+K+K+}{A-A-A-A-A-}$ along capacitor-like membrane
$V_m$ -> $V_{K}$

The $Na^+$ story

$Na^+$/$K^+$ pump pushes $Na^+$ out
$[Na^+]_{in}$ (~10 mM) << $[Na^+]_{out}$ (~140 mM)
Equilibrium potential for $Na^+$, $V_{Na}$ = ~ +55 mV
- Inside positive/outside negative to maintain outside > inside concentration gradient
If $Na^+$ alone, $V_m$ -> $V_{Na}$ (~ +55 mV)

“Resting” potential

Sum of outward $K^+$ and inward $Na^+$
- Membrane more permeable to $K^+$ than $Na^+$, $p_{$K^+}$>$p_{Na+}$
- Outward flow of $K^+$ > inward flow of $Na^+$
- Resting potential (~-70 mV) closer to $V_{K}$ (-90 mV) than $V_{Na}$ (+55 mV)
Goldman-Hodgkin-Katz equation
- $V_m = \frac{RT}{F}ln(\frac{p_{K^+}[K^+]_{out}+p_{Na^+}[Na^+]_{out}}{p_{K^+}[K^+]_{in}+p_{Na^+}[Na^+]_{in}})$

Components

Phase	Neuron State
Resting potential	Passive $K^+$ allow outward flow; passive $Na^+$ allow inward flow; $Na^+$/$K^+$ moves $K^+$ in and $Na^+$ out
Rise to threshold	+ input makes membrane potential more +
Rising phase	Voltage-gated $Na^+$ channels open, $Na^+$ enters
Peak	Voltage-gated $Na^+$ channels close and deactivate; voltage-gated $K^+$ channels open
Falling phase	$K^+$ exits
Refractory period	$Na^+$/$K^+$ pump restores [$Na^+$], [$K^+$]; voltage-gated $K^+$ channels close
Resting potential	Passive $K^+$ allow outward flow; passive $Na^+$ allow inward flow; $Na^+$/$K^+$ moves $K^+$ in and $Na^+$ out

knitr::include_graphics("https://upload.wikimedia.org/wikipedia/commons/thumb/4/4a/Action_potential.svg/300px-Action_potential.svg.png")

knitr::include_graphics("http://hyperphysics.phy-astr.gsu.edu/hbase/Biology/imgbio/actpot4.gif")

Neuron at rest

Driving force on $K^+$ weakly outward
- -70 mV - (-90 mV) = +20 mV
Driving force on $Na^+$ strongly inward
- -70 mV - (+55 mV) = -125 mV
$Na^+$/$K^+$ pump maintains concentrations ($Na^2$ out; $K^+$ in)
- $[K^+]_{i} >> [K^+]_{o}$
- $[Na^+]_{i} << [Na^+]_{o}$

Phase	Ion	Driving force	Flow direction	Flow magnitude
Rest	$K^+$	20 mV	out	small
	$Na^+$	125 mV	in	small

Rising phase

Voltage-gated $Na^+$ channels open
Membrane permeability to $Na^+$ increases
- $Na^+$ inflow through passive + voltage-gated channels
- continued $K^+$ outflow through passive channels

Phase	Ion	Driving force	Flow direction	Flow magnitude
Rising	$K^+$	growing	out	growing
	$Na^+$	shrinking	in	high

Peak

Membrane permeability to $Na^+$ reverts to resting state
- Voltage-gated $Na^+$ channels close & inactivate
- Slow inflow due to small driving force (+30 mV - 55mV = -25 mv)
Membrane permeability to $K^+$ increases
- Voltage-gated $K^+$ channels open
- Fast outflow due to strong driving force (+30 mv - (-90 mv) = +120 mV)

Phase	Ion	Driving force	Flow direction	Flow magnitude
Peak	$K^+$	120 mV	out	high
	$Na^+$	20 mV	in	small

Falling phase

$K^+$ outflow
- Through voltage-gated $K^+$ and passive $K^+$ channels
$Na^+$ inflow
- Through passive channels only

Phase	Ion	Driving force	Flow direction	Flow magnitude
Falling	K	shrinking	out	high
	$Na^+$	growing	in	small

Refractory phase

Absolute

Cannot generate action potential (AP) no matter the size of the stimulus
Membrane potential more negative (-90 mV) than at rest (-70 mV)
Voltage-gated $Na^+$ channels still inactivated
- Driving force on $Na^+$ high (-90 mv - 55 mV = -145 mV), but too bad
Voltage-gated $K^+$ channels closing
- Driving force on $K^+$ tiny or absent
$Na^+$/$K^+$ pump restoring concentration balance

Relative

Can generate AP with larg(er) stimulus
Some voltage-gated $Na^+$ ‘de-inactivate’, can open if
- Larger input
- Membrane potential is more negative than resting potential

Phase	Ion	Driving force	Flow direction	Flow magnitude
Refractory	K	~0 mV	out	small
	$Na^+$	145 mV	in	small

APs and Information Processing

AP amplitudes don’t vary (much)
- All or none
- $V_{K}$ and $V_{Na}$ don’t vary much b/c $Na^+$/$K^+$ pump always working
AP frequency and timing vary
- Rate vs. timing codes
- Same rates, but different timing
- “Grandmother” cells and single spikes

Generating action potentials

Axon hillock
- Portion of soma adjacent to axon
- Integrates/sums input to soma
Axon initial segment
- Umyelinated portion of axon adjacent to soma
- Voltage-gated $Na^+$ and $K^+$ channels exposed
- If sum of input to soma > threshold, voltage-gated $Na^+$ channels open

Propagation

Propagation
- move down axon, away from soma, toward axon terminals.
Unmyelinated axon
- Each segment “excites” the next

Myelinated axon
- AP “jumps” between Nodes of Ranvier –> saltatory conduction
- Nodes of Ranvier == unmyelinated sections of axon
- voltage-gated $Na^+$, $K^+$ channels exposed
- Current flows through myelinated segments
Why does AP flow in one direction, away from soma?
- Soma does not have (many) voltage-gated $Na^+$ channels.
- Soma is not myelinated.
- Refractory periods mean polarization only in one direction.

Conduction velocities

Hodgkin-Huxley Equations

Measuring APs in actual neurons. https://www.youtube.com/embed/k48jXzFGMc8
Interview with Sir Alan Hodgkin, https://www.youtube.com/embed/vSIXbfunHYg
Simulations

Synaptic transmission

Synapse permits neuron to pass electrical or chemical messages to another neuron or target cell (muscle, gland, etc.)

Synapse Types & Locations

Chemical
Electrical
- Gap junctions
- Cytosol (and ionic current) flows through adjacent neurons

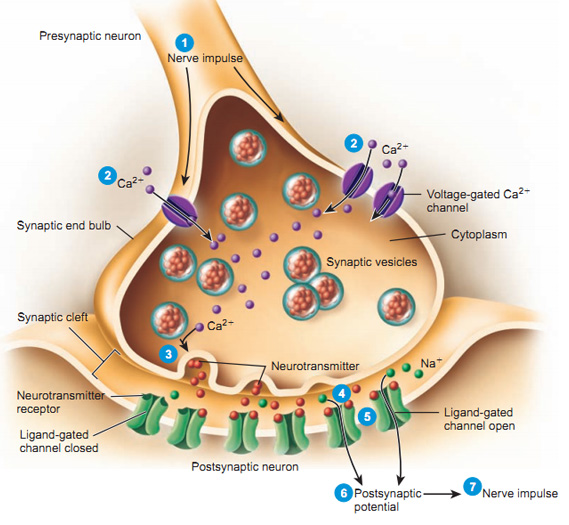
Steps in chemical transmission

Voltage-gated calcium Ca++ channels open
$Ca^{++}$ influx causes synaptic vesicles to bind with presynaptic membrane, fuse with membrane, spill contents via exocytosis

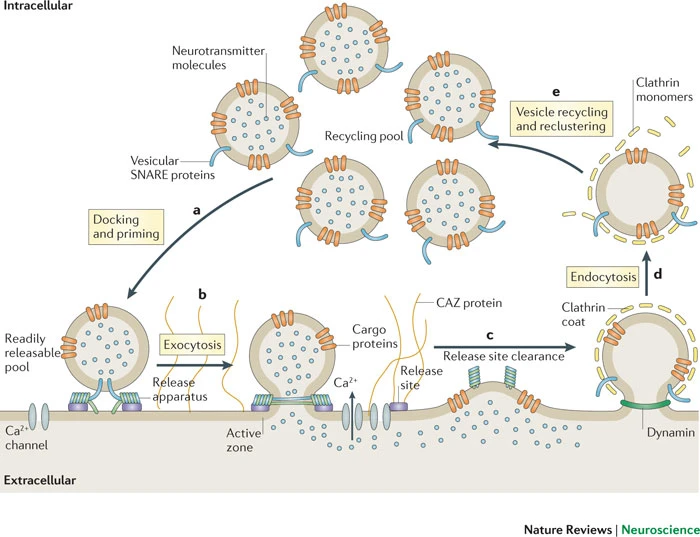
(Figure 1 from Haucke, Neher, & Sigrist, 2011)

knitr::include_graphics("https://ars.els-cdn.com/content/image/1-s2.0-S0143416017301495-fx1.jpg")

NTs diffuse across synaptic cleft
NTs bind with receptors on postsynaptic membrane
- Cause some post-synaptic effect
NTs unbind from receptor
NTs inactivated
NTs diffuse along concentration gradient

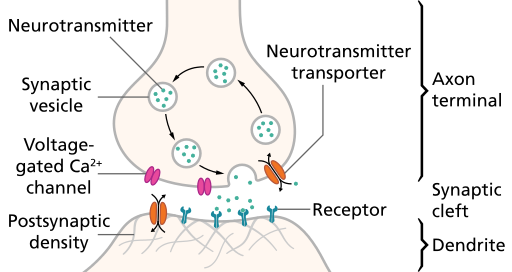
Relative sizes

Neural membrane ~8 nm
Synaptic vesicles ~40-60 or ~90-120 nm
Synaptic cleft ~20-50 nm
Cleft small relative to vesicles

Receptor/channel types

Leak/passive

Vary in selectivity, permeability

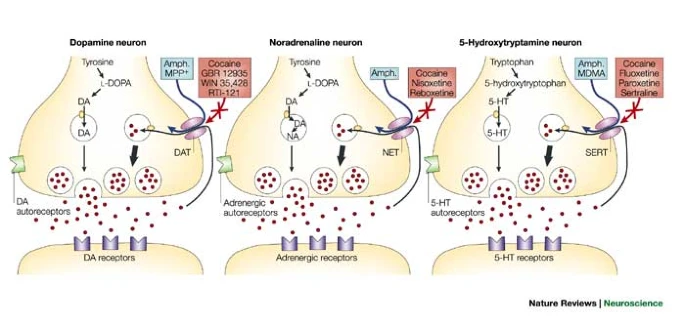
Transporters/exchangers

Ionic
- $Na^+$/$K^+$ ATP-ase/pump
Chemical
- e.g., Dopamine transporter (DAT)

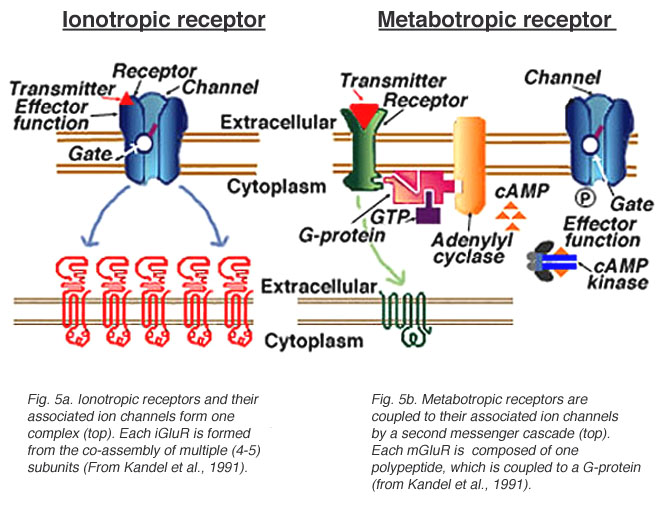
Ionotropic receptors (receptor + ion channel)

Ligand-gated
Open/close channel
Ions flow in/out depending on membrane voltage and ion type
Fast-responding (< 2 ms), but short-duration effects (< 100 ms)

Metabotropic receptors (receptor only)

G-proteins ->
Trigger 2nd messengers
Open/close adjacent channels, change metabolism

http://webvision.med.utah.edu/imageswv/GLU5.jpeg

Receptors generate postsynaptic potentials (PSPs)

Small voltage changes
Amplitude scales with # of receptors activated
Excitatory PSPs (EPSPs)
- Depolarize neuron (make more +)
Inhibitory (IPSPs)
- Hyperpolarize neuron (make more -)

NTs inactivated

Buffering
- e.g., glutamate into astrocytes (Anderson & Swanson, 2000)
Reuptake via transporters
- e.g., serotonin via serotonin transporter (SERT)
Enzymatic degradation
- e.g., acetylcholine esterase (AChE) degrades acetylcholine (ACh)

Questions to ponder

Why do NTs diffuse from pre- to post-synaptic membrane?
Why must NTs be inactivated?
What sort of PSP would opening a $Na^+$ channel produce?
What sort of PSP would opening a $Cl^-$ channel produce?
What sort of PSP would closing a $K^+$ produce?

Synapse location and function

Source: Blausen.com staff https://commons.wikimedia.org/wiki/File%3ABlausen_0843_SynapseTypes.png

on dendrites
- usually excitatory
on cell bodies
- usually inhibitory
on axons
- usually modulatory (change p(fire))

References

Anderson, C. M., & Swanson, R. A. (2000). Astrocyte glutamate transport: Review of properties, regulation, and physiological functions. Glia, 32(1), 1–14. https://doi.org/10.1002/1098-1136(200010)32:1<1::AID-GLIA10>3.0.CO;2-W

Azevedo, F. A., Carvalho, L. R., Grinberg, L. T., Farfel, J. M., Ferretti, R. E., Leite, R. E., et al.others. (2009). Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. Journal of Comparative Neurology, 513(5), 532–541. https://doi.org/10.1002/cne.21974

Boldog, E., Bakken, T. E., Hodge, R. D., Novotny, M., Aevermann, B. D., Baka, J., … Tamás, G. (2018). Transcriptomic and morphophysiological evidence for a specialized human cortical GABAergic cell type. Nature Neuroscience, 21(9), 1185–1195. https://doi.org/10.1038/s41593-018-0205-2

Chung, W.-S., Welsh, C. A., Barres, B. A., & Stevens, B. (2015). Do glia drive synaptic and cognitive impairment in disease? Nature Neuroscience, 18(11), 1539–1545. https://doi.org/10.1038/nn.4142

Eyherabide, H. G., Rokem, A., Herz, A. V. M., Samengo, I., Eyherabide, H. G., Rokem, A., … Samengo, I. (2009). Bursts generate a non-reducible spike-pattern code. Frontiers in Neuroscience, 3, 1. https://doi.org/10.3389/neuro.01.002.2009

Hastoy, B., Clark, A., Rorsman, P., & Lang, J. (2017). Fusion pore in exocytosis: More than an exit gate? A $\beta$-cell perspective. Cell Calcium, 68, 45–61. https://doi.org/10.1016/j.ceca.2017.10.005

Haucke, V., Neher, E., & Sigrist, S. J. (2011). Protein scaffolds in the coupling of synaptic exocytosis and endocytosis. Nature Reviews. Neuroscience, 12(3), 127–138. https://doi.org/10.1038/nrn2948

Moss, S. J., & Smart, T. G. (2001). Constructing inhibitory synapses. Nature Reviews. Neuroscience, 2(4), 240–250. https://doi.org/10.1038/35067500

Torres, G. E., Gainetdinov, R. R., & Caron, M. G. (2003). Plasma membrane monoamine transporters: Structure, regulation and function. Nature Reviews. Neuroscience, 4(1), 13–25. https://doi.org/10.1038/nrn1008

Zeng, H., & Sanes, J. R. (2017). Neuronal cell-type classification: Challenges, opportunities and the path forward. Nature Reviews. Neuroscience. https://doi.org/10.1038/nrn.2017.85